Geometrical proof of identity - II — lesson. Mathematics State Board, Class 7.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

Learn more

Identity

$2$ :

${(a + b)}^{2} = a^{2} + 2ab + b^{2}$

Let us construct a figure of four regions. The two square shaped regions with the dimensions of

$3 × 3$ (Blue) and

$2 × 2$ (Yellow). Observe the remaining two rectangle shaped regions. Both are in

$3 × 2$ (Green) dimension.

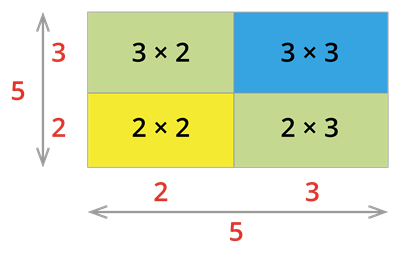
By observing the above rectangle, we can notice that:

$\text{Area of the bigger square = Area of the two small square + Area of the two rectangles}$

$3 + 2$

$2 + 3$

$=$

$(3 × 3) + (2 × 3) + (3 × 3) + (2 × 2)$

Now, we simplify the LHS and RHS of the above expression.

LHS

$=$

$3 + 2$

$2 + 3$

$=$

$5×5 = 25$

RHS

$=$

$(3 × 3) + (2 × 3) + (3 × 3) + (2 × 2)$

$=$

$3^{2} + (2 \times 3) + (3 \times 2) + 2^{2}$

$=$

$9+6+6+4 = 25$

Therefore, LHS

$=$ RHS

Similarly, if we use the variables in this case instead of number we get:

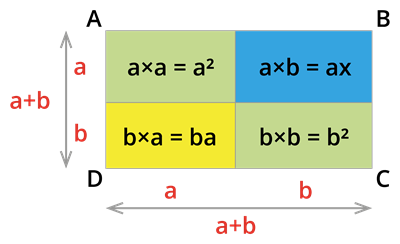
Assume the square of ABCD of side

$a + b$ . From the above figure, we can get that:

$\text{The total area of the bigger square = The area of the two small squares × The are of the two rectangles}$

That is,

$(a + b)^2$

$= a^{2} + ab + ba + b^{2}$

Since,

$ba=ab$ ;

$(a + b)^2$

$= a^{2} + ab + ab + b^{2} = a^{2} + 2 ab + b^{2}$ .

Therefore,

${(a + b)}^{2} = a^{2} + 2ab + b^{2}$ is a identity.

Example:

Simplify the expression

$(a + 6) (a + 6)$ using the identity

${(a + b)}^{2} = a^{2} + 2ab + b^{2}$ .

Now write the given expression

$(a + 6) (a + 6)$ with respect to the given identity

${(a + b)}^{2} = a^{2} + 2ab + b^{2}$ .

$\begin{array}{l} (a + b) (a + b) = (a + 6) (a + 6) \\ {(a + 6)}^{2} = (a^{2} + 2 (6 \times 6) a + 6^{2}) \end{array}$

Now simplify the expression.

$= (a^{2} + 72 a + 36)$ .

Therefore,

$(a + 6) (a + 6)$

$= (a^{2} + 72 a + 36)$ .

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

4. Geometrical proof of identity - II

Theory: