Geometrical proof of the identity - I — lesson. Mathematics State Board, Class 7.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

When it comes to solving the algebraic equation, identities play a vital role to solve them. In this lesson, we are going to explore the geometrical proof of identities.

Let us first see the varies identities which we will discuss here:

$(x + a) (x + b) = x^{2} + x (a + b) + ab$

$(a + b^2) = a^2 + 2ab + b^2$

$(a - b^2) = a^2 - 2ab + b^2$

$(a + b)(a - b) = a^{2} - b^{2}$

Let us take each identity one by one and discuss the proof of that identity.

Identity

$1$ :

$(x + a) (x + b) = x^{2} + x (a + b) + ab$ .

Let us construct a rectangular diagram of four regions. One region is square-shaped with a dimension of

$4 × 4$ (Orange). Also, the other three regions are rectangle in shape with dimensions

$4×2$ (Blue),

$3 × 4$ (Yellow) and

$3 × 2$ (Green).

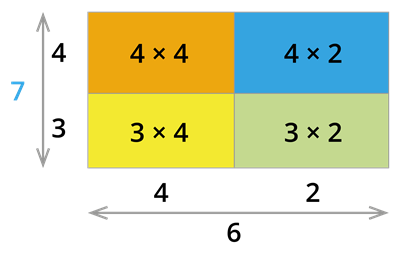
By observing the above rectangle, we can notice that:

$\text{Area of the bigger rectangle}$

$=$

$\text{Area of a square (Orange)}$

$+$

$\text{Area of three rectangles}$

$(4 + 3)$

$(4 + 2)$

$=$

$(4 × 4) + (4 × 2) + (3 × 4) + (3 × 2)$

Now, we simplify the LHS and RHS of the above expression.

LHS

$=$

$(4 + 3)$

$(4 + 2)$

$=$

$7×6 = 42$

RHS

$=$

$(4 × 4) + (4 × 2) + (3 × 4) + (3 × 2)$

RHS

$=$

$16+8+12+6 = 42$

Therefore, LHS

$=$ RHS

Similarly, if we use the variables in this case instead of number we get:

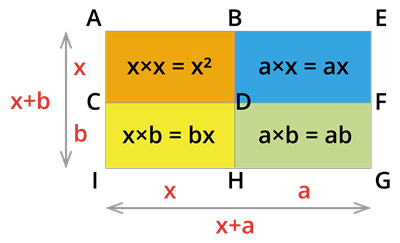
Let one side of a rectangle be

$(x +a)$ , and the other side be

$(x + b)$ units.

Then,

$\text{the total area of the rectangle }AEGI$

$=$

$\text{length } \times \text{breadth}$

$=$

$(x+a)(x+b)$ ………….

$(1)$

$\text{The area of the rectangle }AEGI$

$=$

$\text{The area of the square }ABCD$

$+$

$\text{The area of the rectangle }BEFD$

$+$

$\text{The area of the rectangle }DFGH$

$+$

$\text{The area of the rectangle }CDHI$ .

$\text{The area of the rectangle AEGI}$

$=$

$x^{2} + ax + ab + bx$

$= x^{2} + x (a + b) + ab$ ……………..

$(2)$

From the equation,

$(3)$ and

$(4)$ we get

$(x + a) (x + b) = x^{2} + x (a + b) + ab$ .

Therefore,

$(x + a) (x + b) = x^{2} + x (a + b) + ab$ is a identity.

Example:

Simplify the expression

$(a + 3) (a + 11)$ using the identity

$(x + a) (x + b) = x^{2} + x (a + b) + ab$ .

The expression is

$(a + 3) (a + 11)$ .

Now write the given expression

$(a + 3) (a + 11)$ with respect to the given identity

$(x+a)(x+b)$

$=$

$x^2+(a+b)x+ab$ .

$\begin{array}{l} (x + a) (x + b) = (a + 3) (a + 11) \\ = (a^{2} + a (3 + 11) + 3 \times 11) \end{array}$

Now simplify the expression.

$(a^{2} + 14 a + 33)$ .

Therefore,

$(a + 3) (a + 11)$

$=$

$(a^{2} + 14 a + 33)$ .

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

3. Geometrical proof of the identity - I

Theory: