PDF chapter test TRY NOW
In our previous theory, we understand that the Fibonacci sequence follows a certain pattern.
What is that pattern? How can we visualise it? Let's explore it.
The pattern of the Fibonacci sequence
Let's draw the square of length 1. Then draw one more square length next to the first square.

Now draw the next square below, which is equal to the sum of the first two squares.

Here, we add the side length of the three squares. We get 3. So, next, draw the square which has length 3.

Similarly, the total side length of these squares is 5. So, now draw another square by combining the lengths of all these squares, as shown below.

Follow the same pattern and draw the next square. Then we get the figure as below:

Evidently, we can observe that the obtained length of the squares follows the Fibonacci sequence.
If we draw an arc that connects each opposite side of all the squares, we get a spiral called Fibonacci spiral.
If we draw an arc that connects each opposite side of all the squares, we get a spiral called Fibonacci spiral.

Let's see some interesting GIF of the Fibonacci sequence diagram.
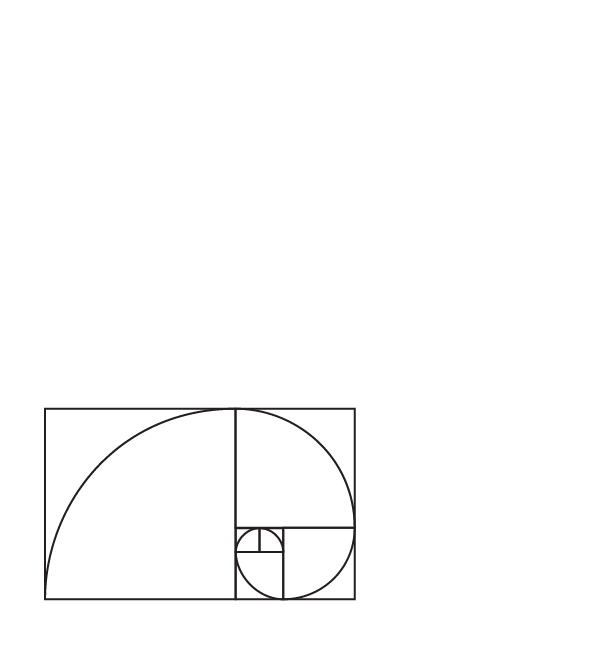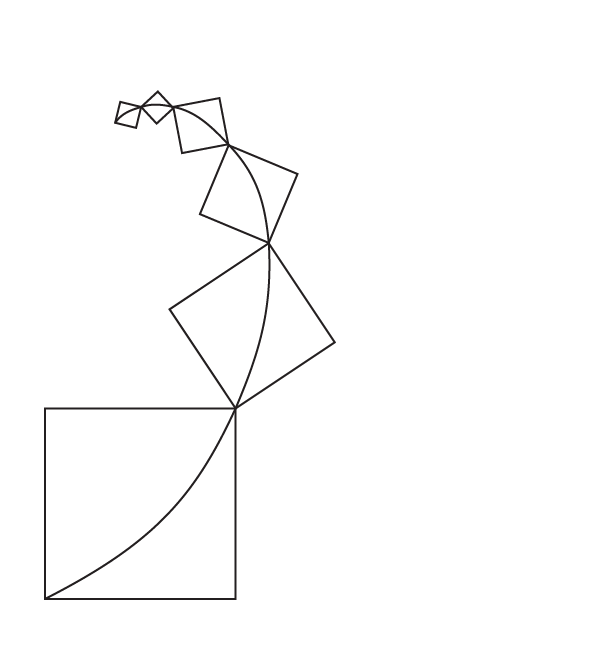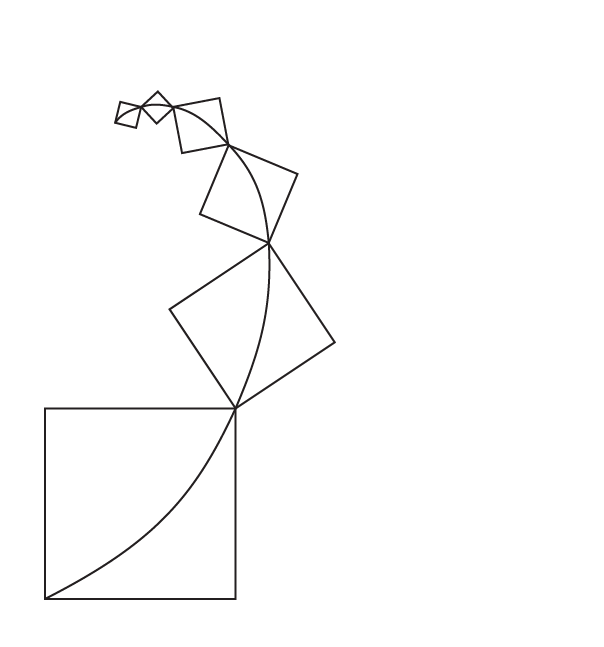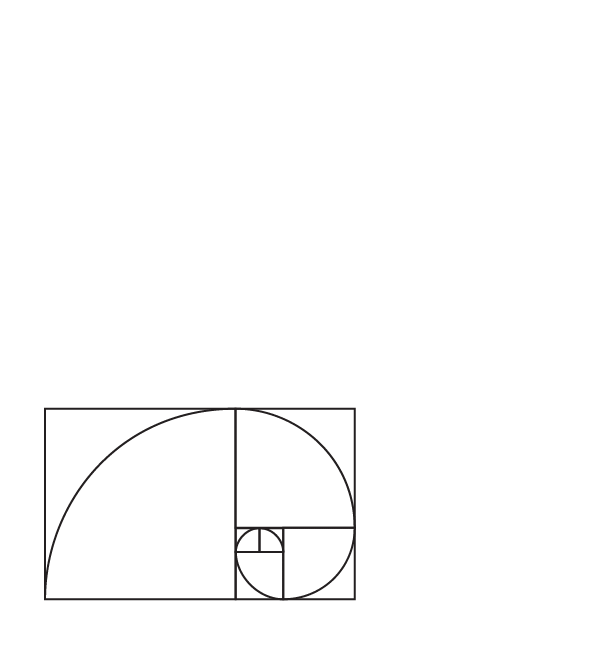
We can see this Fibonacci spiral in nature at many places.
Example:
1. Snail's shell

2. Cyclone structure

3. The universe in a Fibonacci spiral

4. Sunflower seed head

Golden ratio:
Do you know what do the Pyramids of Giza and Da Vinci’s Mona Lisa have in common?
They are all designed using the Golden Ratio!
The Golden Ratio is a mathematical ratio. It is usually found in nature. For decades, the Golden Ratio has been called the most exciting ratio in art and architecture.
- When we take any two successive (one after the other) Fibonacci numbers and divide the larger by the smaller number, the result of dividing the pairs of numbers gives us the approximate value of the Golden ratio “phi” .
- It is represented by the Greek symbol (φ).
- φ = 1.618
Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…,
Let us take the first Fibonacci number as (a), and the consecutive Fibonacci number be (b).
Assume, a = 55; b= 34, then a ÷ b = 55 ÷ 34 = 1.618.
In another way, (a + b) ÷ b also gives the same value.
That is, (a + b) ÷ a = (55 + 34) ÷ 55 = 89 ÷ 55 = 1.618.
Therefore, we can say that a ÷ b = (a + b) ÷ a = φ (phi), where a, and b are consecutive Fibonacci numbers.
Now we divide the Fibonacci number and observe the value we get:

