PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
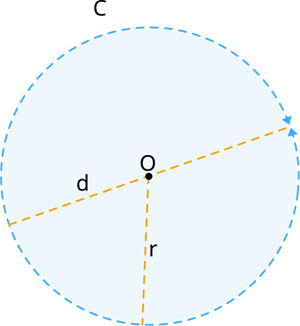
Book Free DemoCircumference of the circle:
The circumference of the circle is defined as the pi(π) multiply with the diameter of the circle(d). The degree of the circle is .
Circumference of the circle = \pi\times d units (where d=2\times r).
= \pi\times 2\times r=2\pi r units
Where .
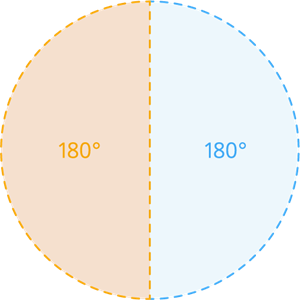
Length of the arc of the semicircular quadrant:
The length of the arc of the semicircular quadrant is defined as the one by two(1/2) pi(π) multiply with the diameter of the circle(d). The degree of the semicircle is 180°.
Circumference of the circle = \pi\times d units (where d=2\times r).
= \pi\times 2\times r=2\pi r units
Length of semicircle arc (l) = \frac{1}{2}\times 2\pi r units.
It can also be written as units (where the degree of semicircle is ).
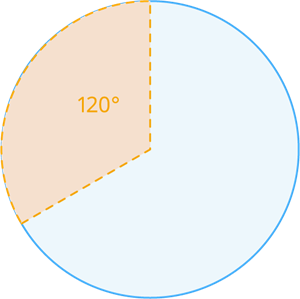
Length of the arc of the one third of the circle:
The length of the arc of the one-third of the circle is defined as the one by three(1/3) pi(π) multiply with the diameter of the circle(d). The degree of the one-third of the circle is 120°.
Circumference of the circle = \pi\times d units (where d=2\times r).
= \pi\times 2\times r=2\pi r units
Length of the one third of the circle arc = \frac{1}{3}\times 2 \pi r units.
It can also be written as units (where the degree of one third of the circle is ).
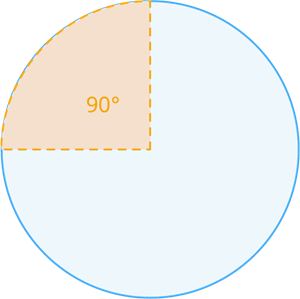
Length of the arc of the circular quadrant:
The length of the arc of the circular quadrant is defined as the one by four or quarter(1/4) pi(π) multiply with the diameter of the circle(d). The degree of the arc of the circular quadrant is 90°.
Circumference of the circle = \pi\times d units (where d=2\times r).
= \pi\times 2\times r=2\pi r units
Length of the quadrant arc(l) = \frac{1}{4}\times 2 \pi r units.
It can also be written as units (where the degree of quadrant is ).
From the above explanation, we get an idea that the length of the arc is equal to the pi(π) multiply with the diameter of the circle(d) by
Therefore the length of the arc .
Important!
If a circle of radius(r) units divided into n equal sectors, then the length of arc = \frac{1}{n}\times 2\pi r units.
Register for free to see more content