UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreArea of circle:
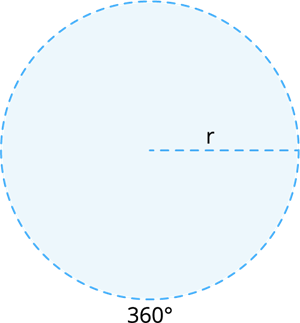
The area of a circle is defined as the number of square units inside that circle. It is pi times the radius square. The degree of the circle is .
Area of circle (\(A\)) \(=\pi r^2\) square units, where .
Area of a semicircle:
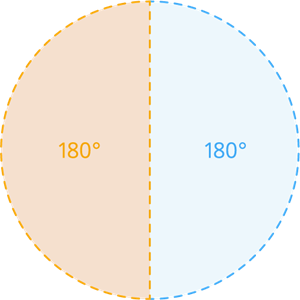
The area of a semicircle is defined as the number of square units inside that circle. It is half(\(1/2\)) pi times the radius square. The degree of the semicircle is \(180°\).
Area of a semicircle \(A=\frac{1}{2}\pi r^2\) square units.
It can also be written as \(\frac{180^\circ}{360^\circ}\pi r^2\) square units (where the degree of semicircle is \(180^\circ\)).
Area of one-third circle:
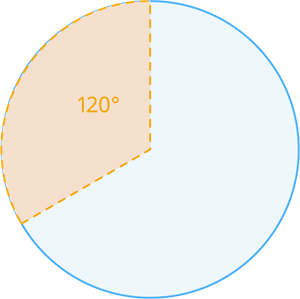
The area of one-third circle is defined as the number of square units inside that circle. It is one by three (\(1/3\)) pi times the radius square. The degree of the one-third circle is \(120°\).
Are of a one - third of circle \(A=\frac{1}{3}\pi r^2\) square units.
It can also be written as square units (where the degree of sector is ).
Area of quadrant circle:
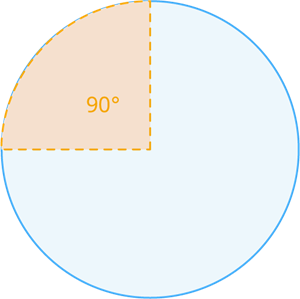
The area of quadrant circle is defined as the number of square units inside that circle. It is one by quarter(\(1/4\)) pi times the radius square. The degree of the quadrant circle is \(90°\).
Area of a quadrant circle \(A=\frac{1}{4}\pi r^2\) square units.
It can also be written as square units (where the degree of quadrant circle is ).
From the above explanation, we get the idea that the area of a sector is equal to the number of square units inside that circle. It is pi time the radius square by where .
Therefore the area of the sector of the circle square units.
Important!
If a circle of radius(\(r\)) units divided into \(n\) equal sectors, then the
area of the sector = \(\frac{1}{n}\times \pi r^2\) square units.
Register for free to see more content