PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us consider the system of linear equations and find the solution graphically.
Find the solution to the system of equations \(2x+y=8\) and \(4x+2y=10\) graphically.
Solution:
Let us consider the equation \(2x+y=8\). Now, we shall substitute the values for \(x\) to find the value of \(y\).
When \(x=1\), \(2(1)+y=8\)\(\Rightarrow y=8-2\)\(\Rightarrow y=6\)
When \(x=2\), \(2(2)+y=8\)\(\Rightarrow y=8-4\)\(\Rightarrow y=4\)
When \(x=3\), \(2(3)+y=8\)\(\Rightarrow y=8-6\)\(\Rightarrow y=2\)
When \(x=4\), \(2(4)+y=8\)\(\Rightarrow y=8-8\)\(\Rightarrow y=0\)
Now, writing these values in the table, we have:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(y\) | \(6\) | \(4\) | \(2\) | \(0\) |
Similarly, plotting the points for the equation \(4x+2y=10\), we have:
When \(x=0\), \(4(0)+2y=10\)\(\Rightarrow 2y=10\)\(\Rightarrow y=5\)
When \(x=1\), \(4(1)+2y=10\)\(\Rightarrow 2y=10-4=6\)\(\Rightarrow y=3\)
When \(x=2\), \(4(2)+2y=10\)\(\Rightarrow 2y=10-8=2\)\(\Rightarrow y=1\)
When \(x=3\), \(4(3)+2y=10\)\(\Rightarrow 2y=10-12=-2\)\(\Rightarrow y=-1\)
Now, writing these values in the table, we have:
| \(x\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(5\) | \(3\) | \(1\) | \(-1\) |
Now, plotting these points in the graph, we have:
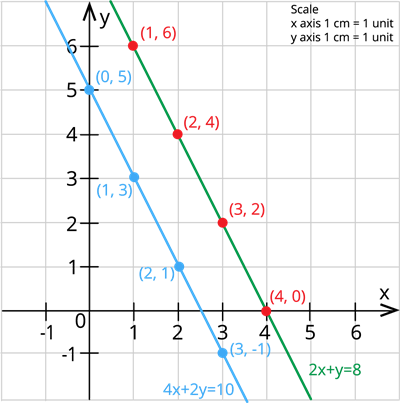
Since the two lines in the graph do not intersect at any point, the graph is said to be an inconsistent system and has no solution.
Another method:
Consider writing the two equations \(2x+y=8\) and \(4x+2y=10\) in the form of \(y = mx + c\) and determine the slope.
Solution:
The slope of the equation \(2x + y = 8\) is given by:
\(y = -2x + 8\)
The slope of the equation \(2x + y = 8\) is \(-2\).
The slope of the equation \(4x + 2y = 10\) is given by:
\(2y = -4x + 10\)
\(y = -2x + 5\)
The slope of the equation \(4x + 2y = 10\) is \(-2\).
Important!
When writing these two equations in the form of \(y = mx+c\), both the equations have the same slope. This proves that the two lines are parallel and does not have a point of intersection.
Register for free to see more content