
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoWhat are simultaneous linear equations?
A set of equations with two or more linear equations having the same variables is called as simultaneous linear equations or system of linear equations or a pair of linear equations.
2x+y=1 and x-y=3
Together they are called as simultaneous linear equations.
Example:
Jane bought 2 apples and 1 banana for a total cost of $8. Let us frame an equation to find the individual cost of an apple and a banana.
Let us understand the purpose of simultaneous linear equations with a real life situation.
Let x denote the cost of an apple and y denote the cost of a banana.
Writing in equation, she has:
2x+y=8 ---- (1)
Jane tries to find the value of each apple and banana by substituting the values for x.
When x=1, 2(1)+y=8\Rightarrow y=8-2\Rightarrow y=6
When x=2, 2(2)+y=8\Rightarrow y=8-4\Rightarrow y=4
When x=3, 2(3)+y=8\Rightarrow y=8-6\Rightarrow y=2
When x=4, 2(4)+y=8\Rightarrow y=8-8\Rightarrow y=0
Now, writing these values in the table, we have:
x | 1 | 2 | 3 | 4 | …. |
| y | 6 | 4 | 2 | 0 | …. |
Jane plots these points in the graph and draws a line joining these points.
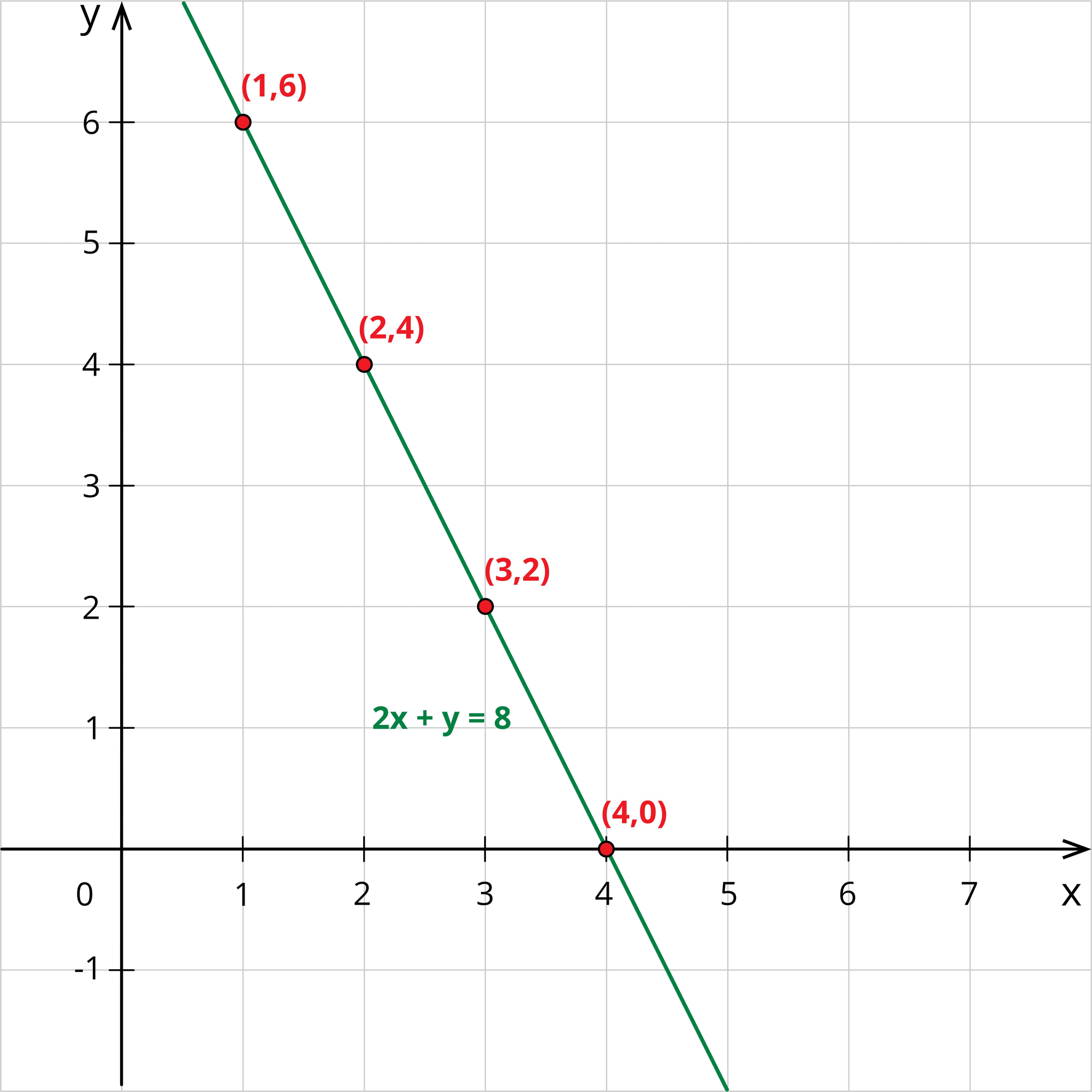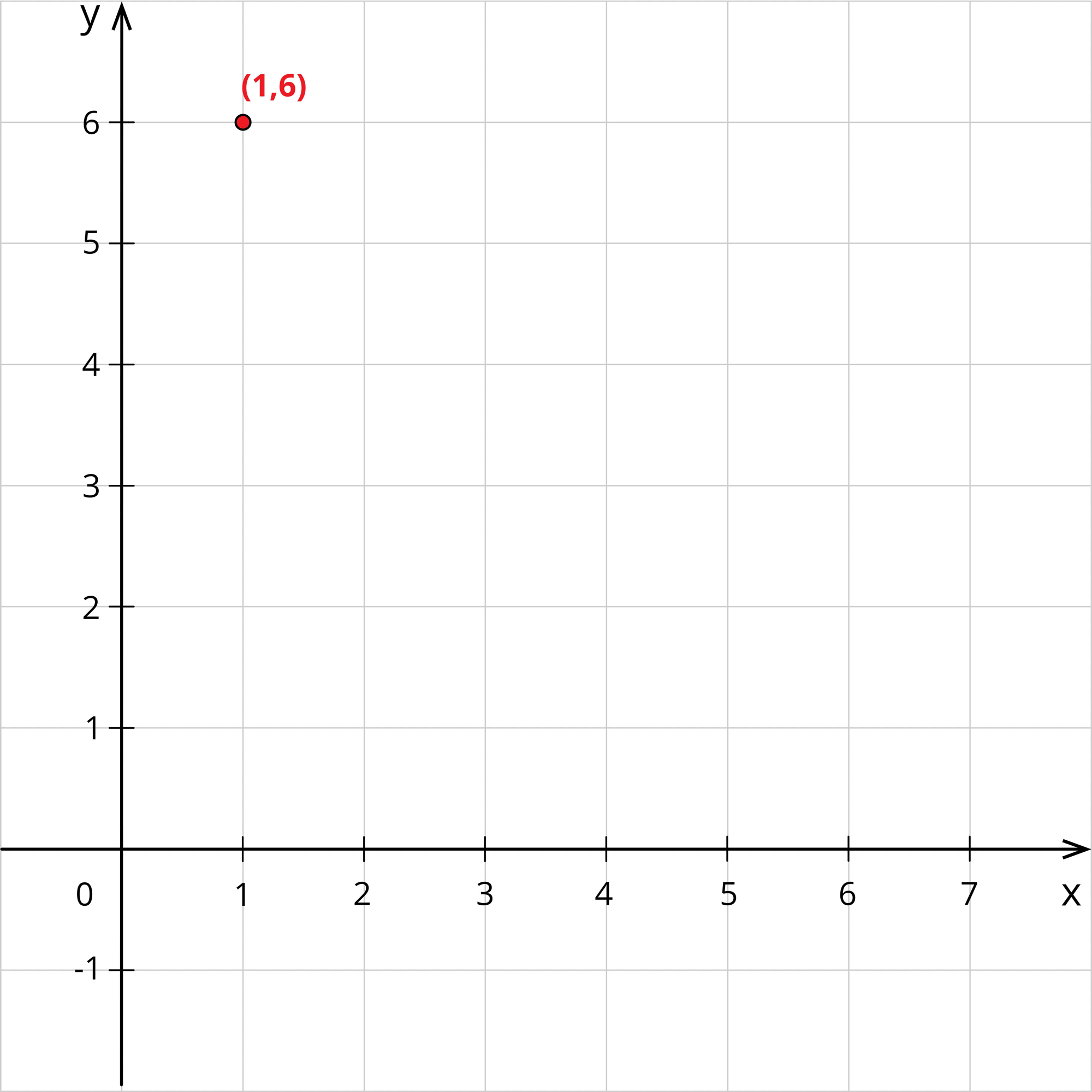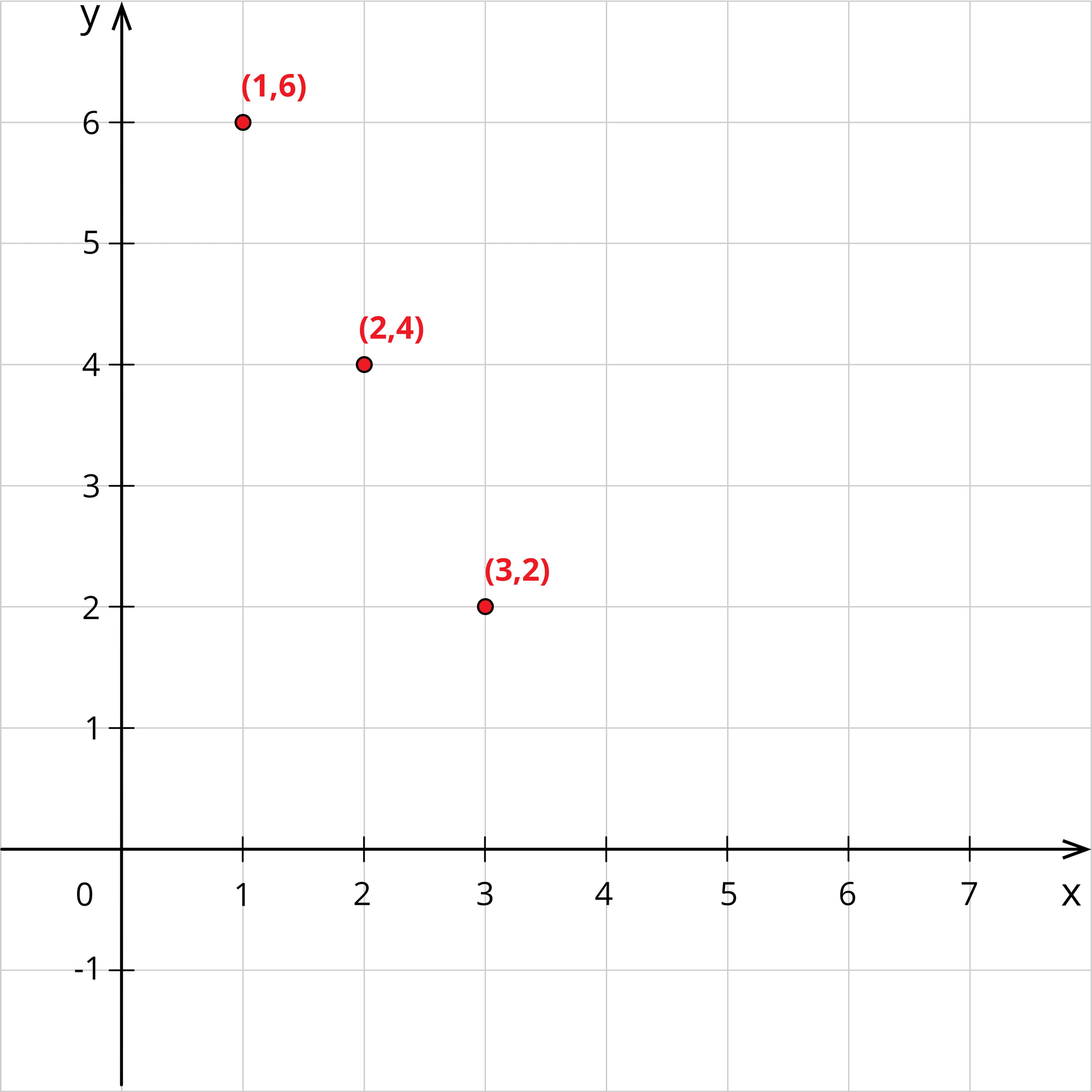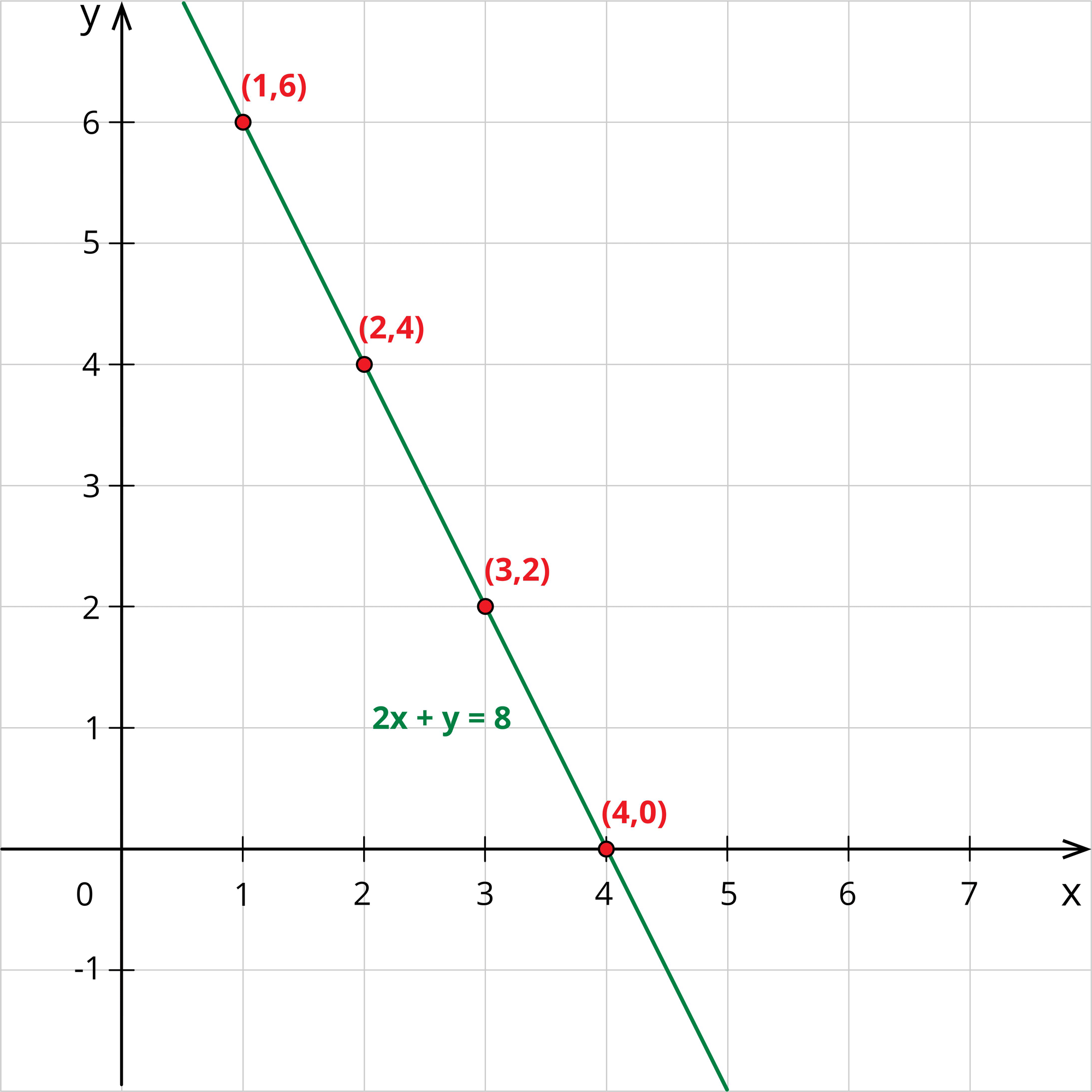
Thus, she gets many number of solutions. Since she is insufficient with the apples and bananas, she again went to the shop and brought 1 apple and 2 bananas for a total cost of ₹10.
Writing in equation, she has:
x+2y=10 ---- (2)
Again, she tries to find each apple and banana's value by substituting the values for x.
When x=1, 1+2y=10\Rightarrow 2y=10-1=9\Rightarrow y=\frac{9}{2}=4.5
When x=2, 2+2y=10\Rightarrow 2y=10-2=8\Rightarrow y=\frac{8}{2}=4
When x=3, 3+2y=10\Rightarrow 2y=10-3=7\Rightarrow y=\frac{7}{2}=3.5
When x=4, 4+2y=10\Rightarrow 2y=10-4=6\Rightarrow y=\frac{6}{2}=3
Now, writing these values in the table, we have:
| x | 1 | 2 | 3 | 4 | …. |
| y | 4.5 | 4 | 3.5 | 3 | …. |
Jane plots these points in the graph and draws a line joining these points.
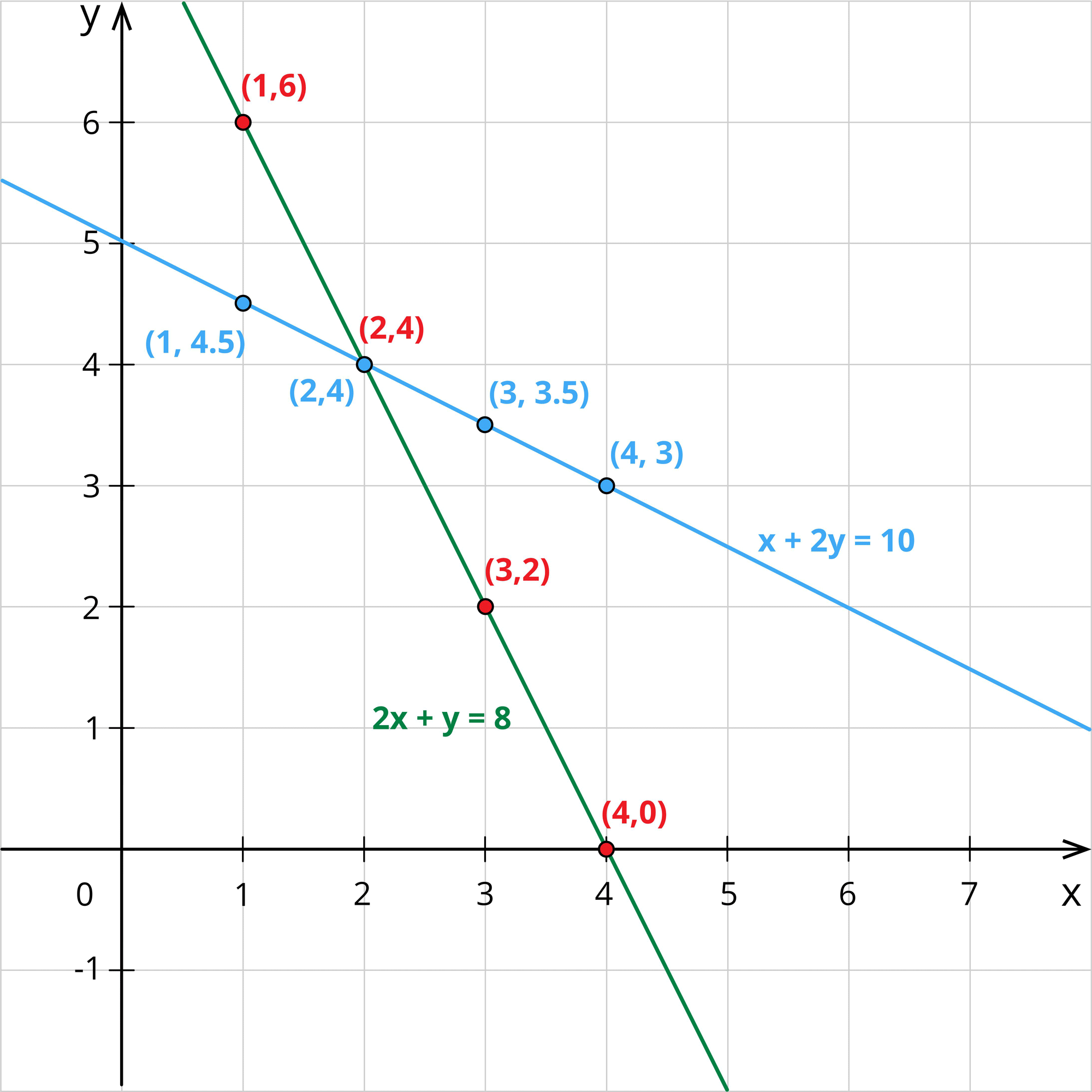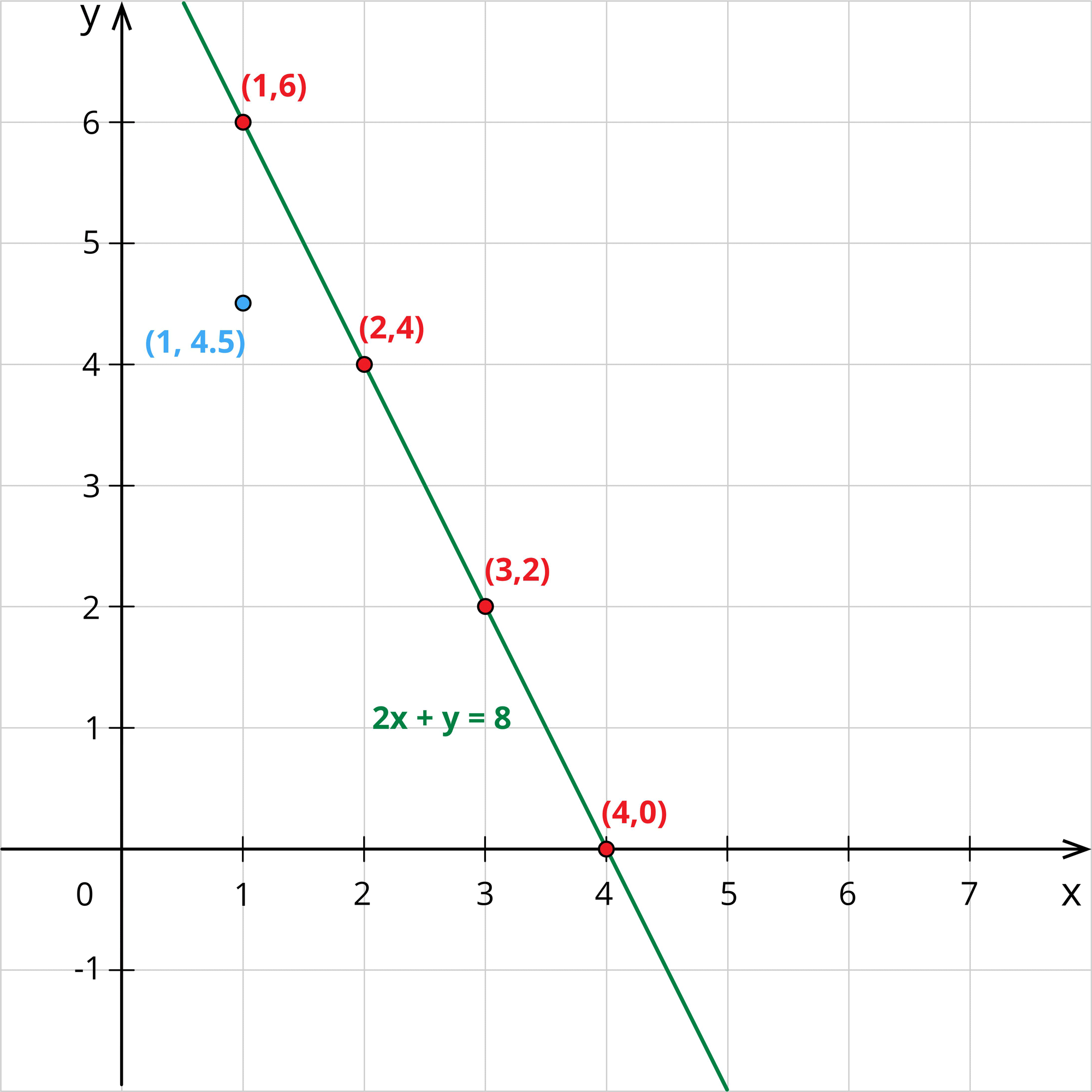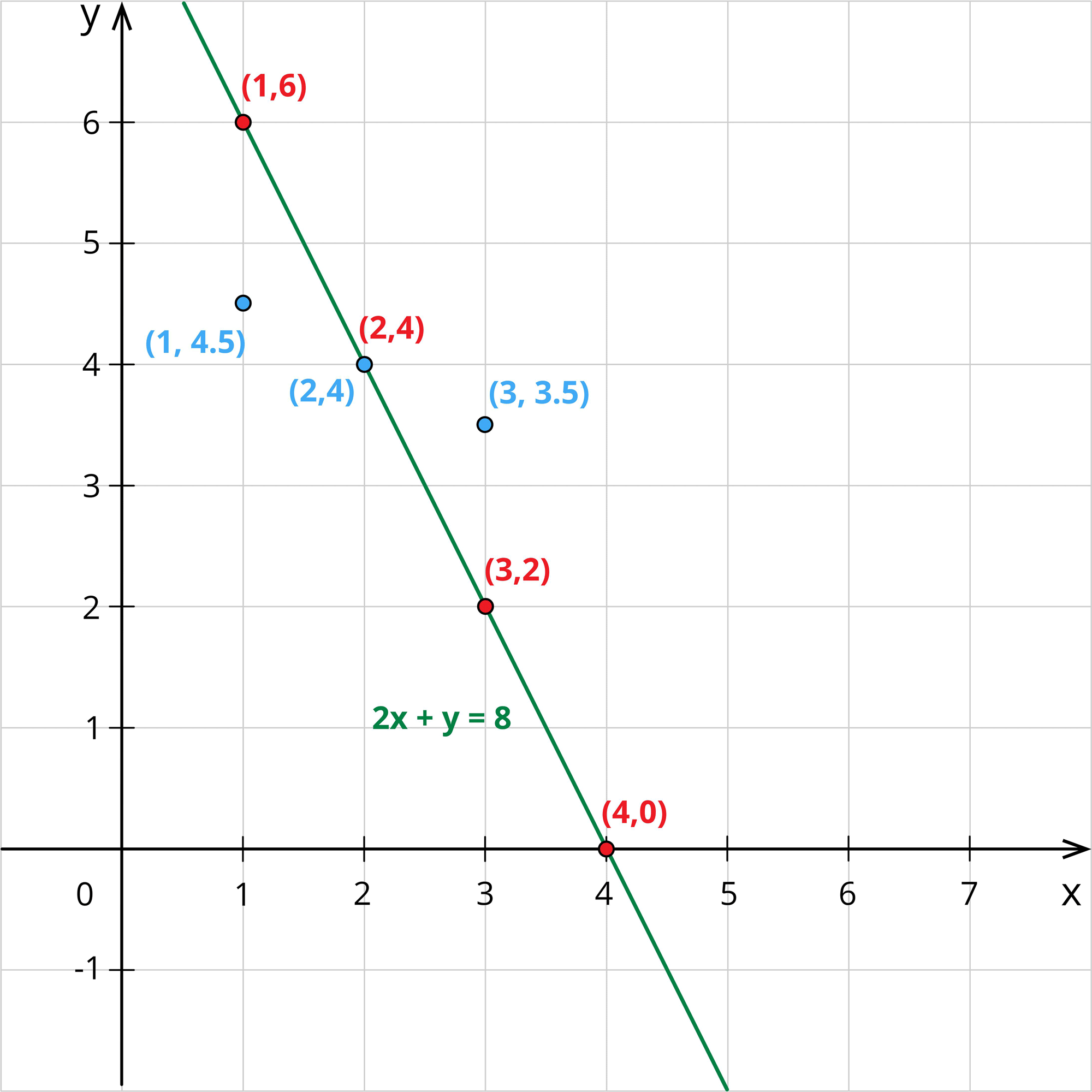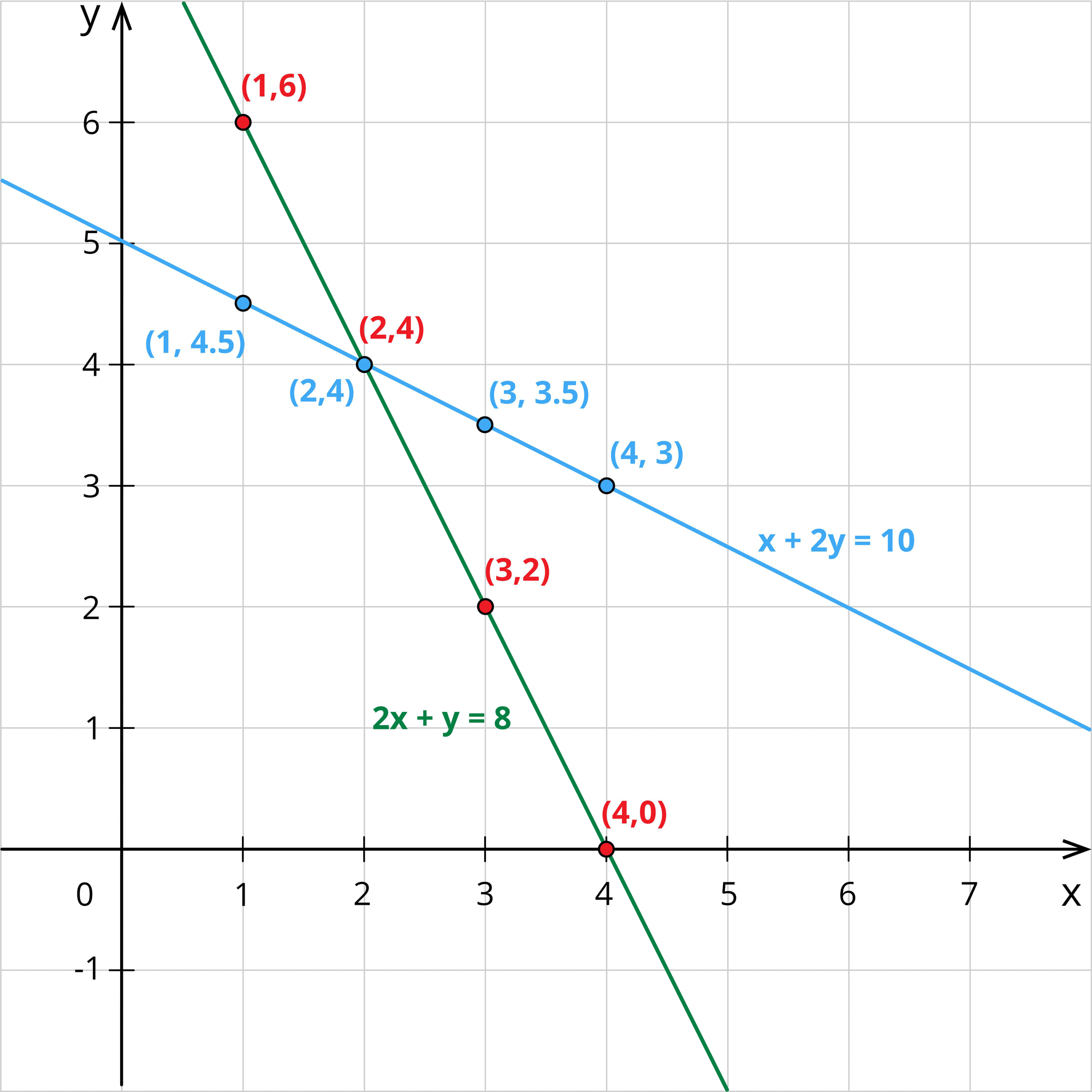
In the graph, she found that the two lines intersect at the point (2,4).
Hence, Jane came to a conclusion that if we solve two equations together, we get an unique solution.
By solving equations (1) and (2), Jane gets the cost of an apple as $2 and the cost of a banana as $4.
These two equations are called as simultaneous linear equations.
Important!
A solution to the simultaneous linear equation can be found in many ways. They are:
1. Graphical method
2. Substitution method
3. Elimination method
4. Cross multiplication method