PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn real life, not every object is in the shape of triangles. Some objects are in the shape of a quadrilateral. We use Heron's formula not only for finding the area of triangles but also we can use it for finding the area of quadrilaterals. For that, we need to divide the quadrilateral into two triangular parts and then use the formula of the area of the triangle.
Let's see one real-life problem based on the shape of quadrilateral.
Example:
Sakthi have one notebook, he tears one paper from the notebook. The torn paper is a kind of quadrilateral \(ABCD\), has \(\angle D = 90^{\circ}\), \(AB = 9 \ cm\), \(BC = 8 \ cm\), \(CD = 5 \ cm\) and \(AD = 12 \ cm\). What is the area of the torn paper?
(Use: \(\sqrt{35} = 5.91\))
Solution:
Given: \(\angle D = 90^{\circ}\), \(AB = 9 \ cm\), \(BC = 8 \ cm\), \(CD = 5 \ cm\) and \(AD = 12 \ cm\)
Construction: Join diagonal \(AC\).
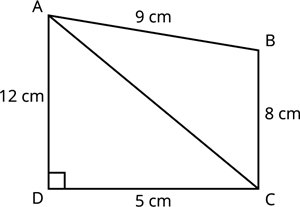
Diagonal \(AC\) divides a quadrilateral into two triangular parts \(ACD\) and \(ABC\).
Now, we need to find the length of \(AC\).
Since \(\angle D = 90^{\circ}\), \(\Delta ACD\) is a right angled triangle.
Using Pythagoras theorem:
\(AC^{2} = AD^{2} + DC^{2}\)
\(AC^{2} = 12^{2} + 5^{2}\)
\(AC^{2} = 144 + 25\)
\(AC^{2} = 169\)
Taking square root on both sides, we get:
\(AC = 13 \ cm\)
Let \(AD = a = 12 \ cm\), \(DC = b = 5 \ cm\) and \(AC = c = 13 \ cm\).
\(cm\)
Area of \(\Delta ADC =\)
\(=\)
\(=\)
\(=\)
\(=\) \(\sqrt{30^2}\)
\(= 30 \ cm^2\)
Now, we need to find the area of \(\Delta ADC\).
Let \(AB = a = 9 \ cm\), \(BC = b = 8 \ cm\) and \(AC = c = 13 \ cm\)
\(cm\)
Area of \(\Delta ABC =\)
\(=\)
\(=\)
\(=\)
\(=\) \(3 \times 2 \sqrt{35}\)
\(=\) \(6 \times 5.91\) \((\) Since \(\sqrt{35} = 5.91)\)
\(= 35.46 \ cm^2\)
Area of \(ABCD =\) Area of \(\Delta ADC +\) Area of \(\Delta ABC\)
\(= 30 + 35.46\)
\(= 65.46 \ cm^2\)
Therefore, the area of the torn paper is \(65.46 \ cm^2\).
Register for free to see more content