5. How to represent irrational number in number line

 
We use the concept of Pythagoras Theorem to form square root numbers.

 

Pythagoras theorem says that 'In a right triangle, the square of the hypotenuse is equal to the sum of the squares of its legs'.

 

Step 1: Draw a number line and label the centre point as zero.

 

Step 2: Mark right side of the zero as \(1, 2, 3,...\) and the left side as \(-1, -2, -3,...\).

 

 

Step 3: Since we need the principal square root value, we won't consider the negative side for measuring.

 

Step 4: Measure the length between \(0\) and \(1\) and draw a line perpendicular to point \(1\) such that the perpendicular line measures \(1\) unit.

 

 

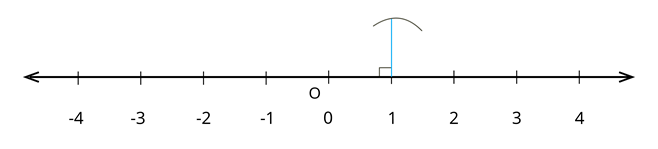
Step 5: Join \(0\) and end of the new line whose length is unity.

 

Step 6: Thus, we got a right-angled triangle.

 

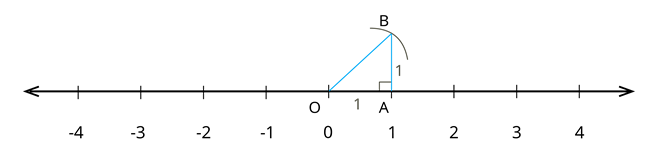
Step 7: Label the triangle and show base, height and the hypotenuse of it.

 

Step 8: Length of the hypotenuse can be determined by applying Pythagoras theorem.

 

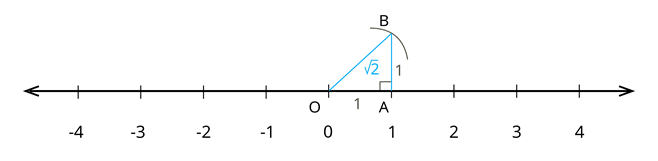
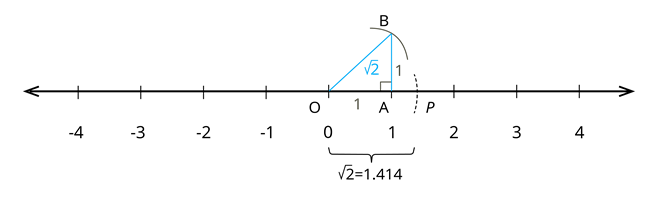
Step 9: Draw an arc on the number line by taking hypotenuse as radius and origin as the centre.

 

Step 10: Thus, the distance between origin and the new arc gives the representation of the square root of \(2\) on the number line. \(OB = OP =\) $\sqrt{2}$.

 

  

Step 11:  Taking the hypotenuse side (length is\) $\sqrt{2}$ as a base and drawing an arc perpendicular to end of hypotenuse by taking a unit length, will result in another right triangle with legs measures $\sqrt{{\left(\sqrt{2}\right)}^2+1^2}=\sqrt{2+1}=\sqrt{3}$

 

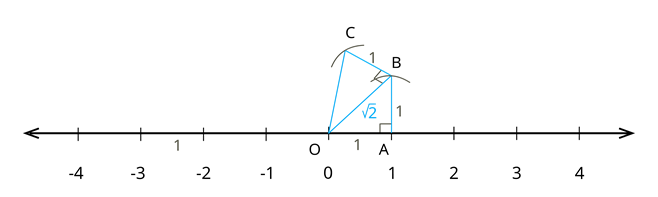
Step 12: Now drawing an arc on the number line by taking the length of the resultant hypotenuse will represent $\sqrt{3}$ on the number line.

 

 

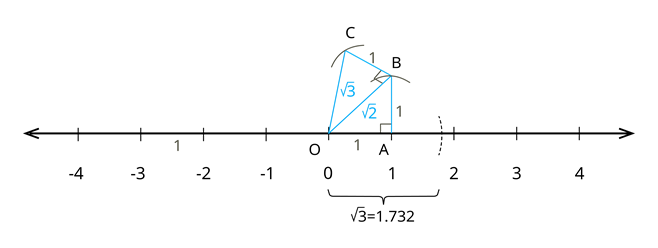
 Step 13: Proceeding in the same way, we can locate $\sqrt{n}$ for any positive integer \(n\), after $\sqrt{n-1}$.