15. திருப்புத்திறன்களின் தத்துவம்

முந்தைய பகுதியில், விசையின் திருப்புத்திறன் செயல்படும் சில எடுத்துக்காட்டுகள் பற்றி அறிந்துகொண்டோம்.

 

இந்த பகுதியில், திருப்புத்திறன்களின் தத்துவம் (principle of moments) பற்றி படிப்போம்.

அல்லது

 

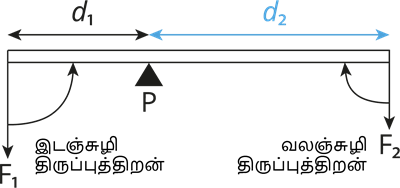
மேற்கண்ட படத்தில் சமநிலையில் உள்ள பொருள் ஒன்றில், ஆதார மையம் $P$ ல் இருந்து $d_1$ தொலைவில் இயங்கும் விசையான $F_1$ இடப்பக்கச் சுழற்சியினையும், ஆதார மையம் $P$ ல் இருந்து $d_2$ தொலைவில் இயங்கும் விசையான $F_2$ வலப்பக்கச் சுழற்சியினையும் ஏற்படுத்துகிறது.

 

விசையின் திருப்புத்திறன் $\tau$ ஆனது,

 

$\tau =\ F \times d$

 

திருப்புத்திறன்களின் தத்துவத்தின் படி,

 

$\text{வலஞ்சுழி திருப்புத்திறன்}\ =\ \text{இடஞ்சுழி திருப்புத்திறன்}$

 

$F_1 \times d_1\ =\ F_2 \times d_2$