
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஇந்த விதியானது 1804 ஆம் ஆண்டில் ஜான் டால்டன் என்ற அறிவியலாளரால் முன்மொழியப்பட்டது.

ஜான் டால்டன்
பெருக்கல் விகித விதி:
A மற்றும் B என்ற இரண்டு தனிமங்கள் ஒன்றாக இனைந்து, ஒன்றுக்கும் மேற்பட்ட சேர்மங்களை உருவாக்கும் பொழுது A ன் நிறையானது B ன் நிறைக்கு படு எளிய விகிதத்தில் சேர்ந்து இருக்கும்.
இதனை விளக்க கீழே உள்ள எடுத்துக்காட்டை காண்போம்.
கார்பன், ஆக்சிஜன் உடன் இனைந்து கார்பன் மோனாக்ஸைடு
(CO) மற்றும் கார்பன் டை ஆக்ஸைடு (CO_2) என்ற இரண்டு ஆக்சைடுகளை தருகிறது.
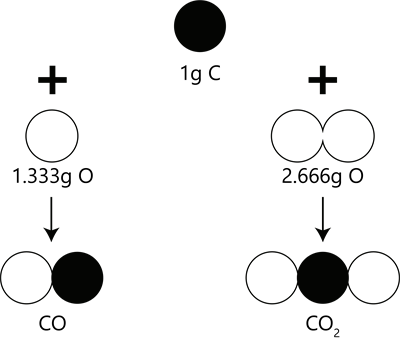
பெருக்கல் விகித விதிக்கு எடுத்துக்காட்டு
சேர்மம் | கார்பன் அணுக்களின் எண்ணிக்கை/நிறை (கி) | ஆக்ஸிஜன் அணுக்களின் எண்ணிக்கை/நிறை (கி) | நிற விகிதங்கள் |
CO | ஒன்று - 12 கி | ஒன்று - 16 கி | 12:16 (அ) 1:1.333 கி |
CO_2 | ஒன்று - 12 கி | ஒன்று - 32 கி | 12:32 (அ)
1:2.666 கி |
ஒரு குறிப்பிட்ட நிறையுள்ள கார்பனுடன், ஆக்சிஜன் சேர்ந்து உருவாகும் கார்பன் மோனாக்சைடு (CO) மற்றும் கார்பன் டை ஆக்சைடு (CO_2) ஆகியவற்றில் உள்ள ஆக்சிஜனின் நிறை விகிதம் 1:2. இது ஒரு எளிய விகிதம் அல்லவா?
மேலும் ஒரு எடுத்துக்காட்டை எடுத்துக் கொள்வோம். சல்ஃபர் ஆக்சிஜனுடன் வினை புரிந்து சல்ஃபர் டை ஆக்சைடு மற்றும் சல்ஃபர் ட்ரை ஆக்சைடை உருவாக்கும். SO_2 மற்றும் SO_3 ஆகியவற்றில் உள்ள ஆக்சிஜனின் நிலையான நிறை விகிதம் 2:3.
இரும்பு, ஃபெர்ரஸ் மற்றும் ஃபெர்ரிக்
குளோரைடு ஆகிய இரண்டு குளோரைடுகளை
உண்டாக்கும். ஒவ்வொரு குளோரைடும் 2 கி
இரும்பிலிருந்து தயாரிக்கப்பட்டது. 4.538 கி ஃபெர்ரஸ் குளோரைடு மற்றும் 5.804 கி ஃபெர்ரிக் குளோரைடு உண்டாகின்றது.
இது பெருக்கல் விகித விதியைப் பொருத்தது
என்பதை காட்டுக.
எடுத்துக்கொண்ட இரும்பின் எடை இரண்டு விதத்திலும் சமமாகும். அதாவது 2.0 கி. ஆகவே
இந்தசேர்மத்தில் குளோரின் விகிதம் 1.5 அல்லது 2:3.
ஃபெர்ரஸ் குளோரைடு | : | ஃபெர்ரிக் குளோரைடு |
2.538 | : | 3.804 |
1 | : | 1.5 or 2:3 |
குளோரின் எடை எளிய விகிதத்தின் மூலம் காட்டபட்டுள்ளது. இதன் மூலம் பெருக்கல் விகித விதி சரிபார்க்க பட்டுள்ளது.