PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo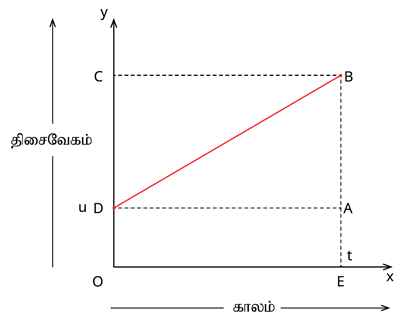
திசைவேகம் காலம் மாறுபாடு
‘D’ என்ற தொடக்கப் புள்ளியிலிருந்து ‘u’ என்ற திசை வேகத்துடன் இயங்கும் ஒரு பொருளின் திசைவேகம் தொடர்ச்சியாக அதிகரித்து ‘t’ காலத்திற்குப் பின் ‘B’ என்ற புள்ளியை அப்பொருள் அடைகிறது.
\text{பொருளின் தொடக்கத் திசைவேகம்} = u = OD = EA
\text{பொருளின் இறுதித் திசைவேகம்} = v = OC = EB
\text{காலம்} = t = OE = DA
வரைபடத்திலிருந்து, ‘t’ காலத்தில் பொருள் ஒன்று கடந்த தொலைவான நாற்கரத்தின் பரப்பளவு DOEB மூலம் கொடுக்கப்படுகிறது.
S = \text{நாற்கரத்தின் பரப்பளவு} ( DOEB)
S = \text {செவ்வகத்தின் பரப்பளவு} (DOEA) + \text{முக்கோணத்தின் பரப்பளவு} (DAB)
S =
வரைபடத்திலிருந்து,
AE = u,
OE = DA = t ,
AB = a
எனவே,
---------------- (2)
இது இரண்டாம் இயக்கச் சமன்பாடு ஆகும்.
Register for free to see more content