PDF chapter test TRY NOW
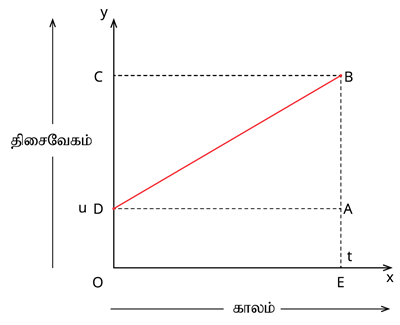
தொலைவு காலம் வரைப்படம்
‘D’ என்ற தொடக்கப் புள்ளியிலிருந்து ‘u’ என்ற திசை வேகத்துடன் இயங்கும் ஒரு பொருளின் திசைவேகம் தொடர்ச்சியாக அதிகரித்து ‘t’ காலத்திற்குப் பின் ‘B’ என்ற புள்ளியை அப்பொருள் அடைகிறது.
\text{பொருளின் தொடக்க திசைவேகம்} = u = OD = EA
\text{பொருளின் இறுதித் திசைவேகம்} = v = OC = EB
\text{காலம்}= t = OE = DA
இங்கு,
DOEB என்பது சரிவகத்தை குறிக்கிறது.
s = \text {சரிவகம் DOEB யின் பரப்பளவு}
s = \times \text{இணைப் பக்க நீளங்களின் கூடுதல்} \times \text{இணைப் பக்கங்களுக்கு இடைப்பட்ட தொலைவு}
s = ------------------------ (1)
ஆனால்,
\text{முடுக்கம் (a)} = அல்லது t = ___________(2)
எனவே,
சமன்பாடு 1 ல் சமன்பாடு 2 ன் மதிப்பை பிரதியிடவும்,
s =
s =
2as =
இங்கு,
எனவே,
2as =
___________ (3)
இது மூன்றாம் இயக்கச் சமன்பாடு ஆகும்.
