PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஒரு பொருளின் திசைவேகத்தில் சீரான கால இடைவெளியில் காலத்தினைப் பொருத்து ஏற்படும் மாற்றம் (அதிகரித்தல் அல்லது குறைதல்) சீரானதாக இருப்பின் அம்முடுக்கம் சீரான முடுக்கம் எனப்படும்.
- நேரான ஒரு சாலையில் பயணிக்கும் ஒரு மகிழுந்தை கருதுவோம்.
- மகிழுந்தின் திசைவேகமானது ஒவ்வொரு 5 விநாடிக்கும் அதன் வேகமானியின் மூலம் பதிவு செய்யப்படுவதாக கருதுவோம்.
வெவ்வேறு கால இடைவெளியில் மகிழுந்தின் திசைவேகம் (\text{மீ/வி}) அட்டவணையில் பின்வருமாறு கொடுக்கப்பட்டுள்ளது.
காலம் (விநாடி) | மகிழுந்தின் திசைவேகம் (மீ/விநாடி) |
0 | 0 |
5 | 9 |
10 | 18 |
15 | 27 |
20 | 36 |
25 | 45 |
30 | 54 |
மகிழுந்தின் இயக்கத்திற்கான திசைவேகம்- காலம் வரைபடம் கீழே காட்டப்பட்டுள்ளது.
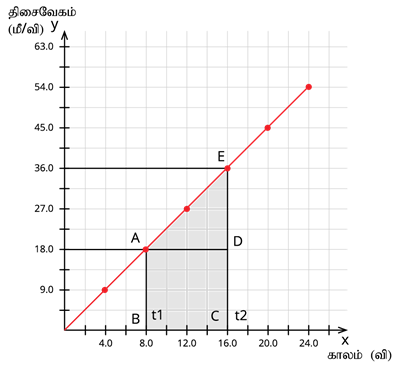
திசைவேகம்- காலம் வரைபடம்
- இங்கு, சம கால இடைவெளியில் திசைவேகமானது சம அளவு மாறுபடுவதை வரைபடம் காட்டுகிறது.
- ஆகவே, சீரான முடுக்கப்பட்ட இயக்கங்கள் அனைத்திற்கும் திசைவேகம்-காலம் வரைபடம் ஒரு நேர்கோடாக அமையும் என்பது தெளிவாகிறது.
- திசைவேகம் - காலம் வரைபடத்திலிருந்து மகிழுந்து எவ்வளவு தொலைவு சென்றுள்ளது என்பதையும் கண்டுப்பிடிக்க முடியும்.
- திசைவேகம் - காலம் வரைபடத்தில் உள்ள பரப்பளவானது, மகிழுந்து கொடுக்கப்பட்ட கால இடைவெளியில் கடந்து சென்ற தொலைவை அதாவது இடப்பெயர்ச்சியின் எண்மதிப்பைக் குறிக்கிறது.
- மகிழுந்தின் திசைவேகத்தின் எண்மதிப்பு, அதன் முடுக்கத்தினால் மாறுவதால் மகிழுந்தானது பயணம் செய்த தொலைவு, திசைவேகம் - காலம் வரைபடத்தில் உள்ள பரப்பளவு ABCDE மூலம் கிடைக்கும்.
S = \text{பரப்பளவு} ABCDE
S = \text{செவ்வகத்தின் பரப்பளவு ABCD} + \text {முக்கோணத்தின் பரப்பளவு ADE}
\text{நாற்கரம்} ABCDE இன் பரப்பளவை, \text {சரிவகம்} ABCDE இன் பரப்பளவிலிருந்தும் கணக்கிட முடியும். அதாவது,
S = \text{சரிவகம்} ABCDE \text{யின் பரப்பளவு}
S = \text{இணைப்பக்க நீளங்களின் கூட்டல்} × \text {இணைப்பக்கங்களுக்கு இடைப்பட்ட தொலைவு}
கீழ்க்கண்ட வரைபடத்தில் காட்டப்பட்டுள்ளது போல சீரற்ற முடுக்குவிக்கப்பட்ட இயக்கத்தில், தொலைவு - காலம் மற்றும் திசைவேகம் - காலம் வரைபடங்கள் எந்த ஒரு வடிவத்தையும் கொண்டிருக்கும்.
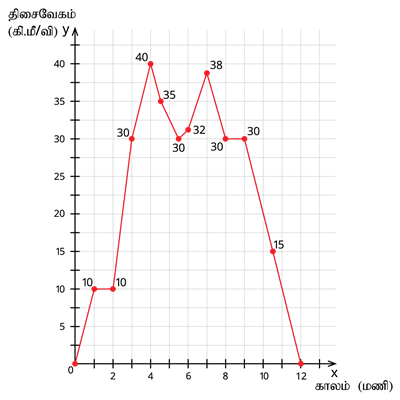
திசைவேகம் - காலம் வரைபடம்
Important!
வாகனத்தில் உள்ள வேகமானி ஒரு குறிப்பிட்ட கண நேரத்தில் நிகழும் வேகத்தை அளக்கும். ஒரு பரிமாண சீரான இயக்கத்தில் சராசரித் திசைவேகமும் உடனடித் திசைவேகமும் சமம். எந்த ஒரு கணத்திலும் கணக்கிடப்படும் உடனடித் திசைவேகம் என்பதை அப்பொருளின் திசைவேகம்என்றும், உடனடிவேகம் என்றும், வேகம் என்றும் கூறலாம்.
Register for free to see more content