PDF chapter test TRY NOW
நேரிய சார்புகளுக்கான வரைபடங்களை அடையாளம் காணுதல்.
நேரிய சார்பு
f: \mathbb{R} \rightarrow \mathbb{R} என்ற சார்பு f(x) = mx + c, m \neq 0 என வரையறுக்கப்பட்டால் அது நேரிய சார்பு ஆகும்.
நேரிய சார்பின் வரைபடம் நேர்க்கோடு ஆகும்.
ஒரு சில குறிப்பிட்ட நேரிய சார்புகள் மற்றும் அதன் வரைபடங்கள் பற்றி காணலாம்.
- சமனிச் சார்பு
- கூட்டல் தலைகீழிச் சார்பு
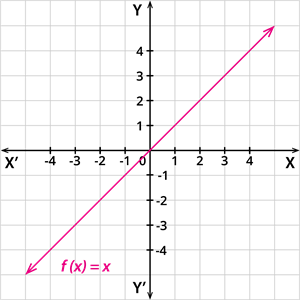
சமனிச் சார்பு
f: \mathbb{R} \rightarrow \mathbb{R} என்ற சார்பு f(x) = x என வரையறுக்கப்பட்டால் அது சமனிச் சார்பு ஆகும்.
சமனிச் சார்பின் வரைபடம்:
 |
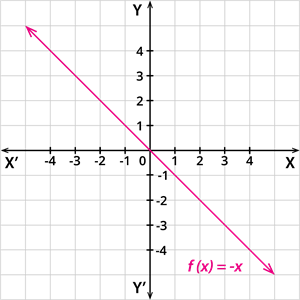
கூட்டல் தலைகீழிச் சார்பு
f: \mathbb{R} \rightarrow \mathbb{R} என்ற சார்பு f(x) = - x என வரையறுக்கப்பட்டால் அது கூட்டல் தலைகீழிச் சார்பு ஆகும்.
கூட்டல் தலைகீழிச் சார்பின் வரைபடம்:
 |
Important!
நேரிய சார்பு எப்பொழுதும் ஒன்றுக்கு ஒன்று சார்பாகும்.
Register for free to see more content