PDF chapter test TRY NOW
ஒரு முக்கோணத்தின் எவையேனும் இரு பக்கங்கள் கொடுக்கப்பட்டிருப்பின் மூன்றாவது பக்கமானது, இரு பக்கங்களின் வித்தியாசம் மற்றும் கூடுதல் ஆகியவற்றின் இடையில் அமையும்.
இங்கு,
a - b < c
b - c < a மற்றும்
c - a < b
Example:
AB = c = 3 செ.மீ, BC = a = 4 செ.மீ மற்றும் AC = b =5 செ.மீ கொண்ட ABC என்ற முக்கோணத்தை எடுத்துக்கொள்வோம்.
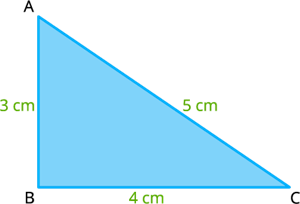
ABC என்ற முக்கோணத்தின் சமனின்மை பண்பை சரிபார்க்கலாம்,
a - b = 4 - 5 = -1 < 3 = c
b - c = 5 - 3 = 2 < 4 = a மற்றும்
c - a = 3 - 4 = -1 < 5 = b
Important!
a, b மற்றும் c என்பன முக்கோணத்தின் பக்கங்கள், a மற்றும் b என்பன தெரிந்த பக்கங்கள் c என்பது தெரியாத பக்கம் எனில் முக்கோணத்தின் சமனி பண்பின் மூலம் முக்கோணத்தின் மூன்றாவது பக்கத்தைக் காணலாம். மூன்றாவது பக்கம் c இன் மதிப்பு கூடுதல் (a+b) இன் மதிப்பை விட குறைவாக இருக்கும் மற்றும் வித்தியாசம் (a-b) மதிப்பை விட குறைவாக இருக்கும். எனவே, (c) இன் மதிப்பு வித்தியாசம் (a-b) மற்றும் கூடுதல் (a+b)க்கு இடையில் இருக்கும்.
Register for free to see more content