PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoமுக்கோணத்தின் வகைகள் பற்றி காணலாம்:
பக்கங்கள் மற்றும் கோணங்களின் அடிப்படையில் முக்கோணத்தினை பல வகைகளாகப் பிரிக்கலாம்.
பக்கங்களின் அடிப்படையில் முக்கோணத்தின் வகைகள்:
- சமபக்க முக்கோணம்
- இருசமபக்க முக்கோணம்
- அசமபக்க முக்கோணம்
ஒரு முக்கோணத்தின் மூன்று பக்கங்களும் சம அளவுடையவை எனில் அது ஒரு சமபக்க முக்கோணம் ஆகும்.
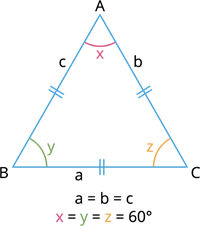
Example:
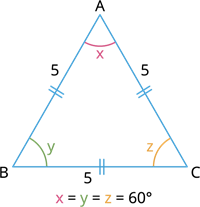
இங்கு, அனைத்து பக்கங்களும் சமம்.
அதாவது, \(AB = BC = CA = 5\) அலகுகள்.
ஒரு முக்கோணத்தில் எைவயேனும் இரண்டு பக்கங்கள் சம அளவுடையவை எனில் அது ஓர் இருசமபக்க முக்கோணம் ஆகும்.
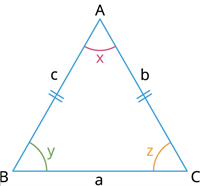
Example:
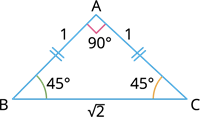
இங்கு, இரண்டு பக்கங்கள் சமம்.
அதாவது, \(AB=CA=1\) அலகு மற்றும்\(BC=√2\) அலகுகள்.
ஒரு முக்கோணத்தின் மூன்று பக்கங்களும் வெவ்வேறு அளவுடையவை எனில் அது ஓர்
அசமபக்க முக்கோணம் ஆகும்.
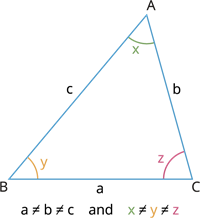
Example:
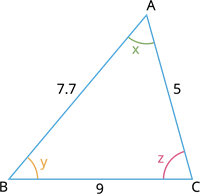
இங்கு, மூன்று பக்கங்களும் வெவ்வேறு அளவுடையவை.
அதாவது, \(AB=7.7, CA=5\) அலகுகள் மற்றும்\(BC=9\) அலகுகள்.
கோணங்களின் அடிப்படையில் முக்கோணத்தின் வகைகள்:
- குறுங்கோண முக்கோணம்
- செங்கோன முக்கோணம்
- விரிகோண முக்கோணம்
ஒரு முக்கோணத்தின் மூன்று கோணங்களும் குறுங்கோணங்களாக (\(0^\circ\) இக்கு மேல் \(90^\circ\) இக்குள்) இருப்பின் அது ஒரு குறுங்கோண முக்கோணம் ஆகும்
Example:
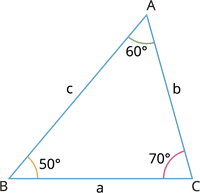
இங்கு, முக்கோணத்தின் அனைத்து கோணங்களும் \(90^\circ\) விட குறைவு ஆகும். அதாவது \(∠A = 60^\circ, ∠B = 50^\circ\) மற்றும் \(∠C = 70^\circ\).
ஒரு முக்கோணத்தின் ஏதேனும் ஒரு கோணம் செங்கோணமாக \((90^\circ)\) இருப்பின் அது ஒரு செங்கோண முக்கோணம் ஆகும்.
Example:
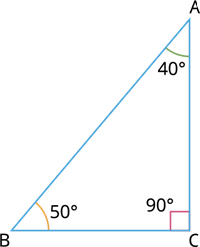
இங்கு, \(∠A = 40^\circ, ∠B = 50^°\) மற்றும் \(∠C = 90^°\).
எனவே, இது ஒரு செங்கோண முக்கோணம் ஆகும்.
ஒரு முக்கோணத்தின் ஏதேனும் ஒரு கோணம் விரிகோணமாக (\(90^°\) இக்கு மேல் \(180^°\)இக்குள்) இருப்பின் அது ஒரு விரிகோண முக்கோணம் ஆகும்.
Example:
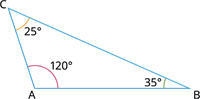
இங்கு, ஒரு கோணம் \(90^°\) விட அதிகமாக உள்ளது.
அதாவது, \(∠A = 120^°, ∠B = 35^°\) மற்றும் \(∠C = 25^°\).
Register for free to see more content