PDF chapter test TRY NOW
அறிவியல் குறியீடு
ஒரு மிகப்பெரிய அல்லது மிகச்சிறிய எண்களை தசமக் குறியீட்டில் வடிவமைக்கும் ஒரு வழிமுறை அறிவியல் குறியீடு எனப்படும். 1 \leq a <10 மற்றும் n எனில்இதை N = a \times 10^n என்று குறிப்பிடலாம்.
1,08,00,00,000 \ km/hr என்ற விளக்கின் வேகத்தை எடுத்துக்கொள்வோம் . இதில் எத்தனை பூச்சியங்கள் உள்ளது என்பதை கணக்கிடுவது கடினம். எனவே 1,08,00,00,000 \ km/hr என்ற எண்ணை 1.08 \times 10^9 என்ற அறிவியல் குறியீட்டால் குறிப்பிடலாம். இந்த வகையான குறியீடு அறிவியல் குறியீடு எனப்படுகிறது.
அறிவியல் குறியீட்டில் தசம எண்களை எழுதுதல்
ஓர் எண்ணை அறிவியல் குறியீட்டால் எழுத கீழ்க்காணும் வழிமுறைகளை பயன்படுதலாம்:
1. தசமப் புள்ளிக்கு இடப்பக்கம் ஒரேயொரு பூச்சியமற்ற எண் இருக்குமாறு, தசமப் புள்ளியை நகர்த்துக.
2. பழைய தசமப் புள்ளிக்கும் புதிய தசமப் புள்ளிக்கும் இடையில் உள்ள இலக்கங்களின் எண்ணிக்கையை கணக்கிட்டு 10-ன் அடுக்கில் எழுத வேண்டும.
3. தசமப் புள்ளியானது இடப்பக்கம் நகர்த்தப்பட்டிருந்தால் அடுக்கு மிகை எண் ஆகும். தசமப் புள்ளியானது வலப்பக்கம் நகர்த்தப்பட்டிருந்தால் அடுக்கு குறை எண் ஆகும்.
Example:
கீழ்க்கண்டவற்றை அறிவியல் குறியீட்டில் எழுதுக : (i) 2839507233 (ii) 0.00003794
தீர்வு:
(i) தசமப் புள்ளியை இடப்பக்கமாக நகர்த்தினால் கிடைப்பது:
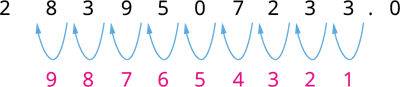
புள்ளியானது 9 இடங்கள் இடப்பக்கமாக நகர்த்தப்பட்டுள்ளது. எனவே, இதன் அறிவியல் குறியீடு 2.839507233 \times 10^9 ஆகும்.
(ii) தசமப் புள்ளியை வலப்பக்கமாக நகர்த்தினால் கிடைப்பது:
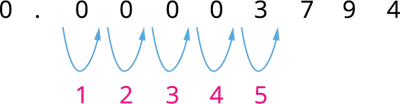
புள்ளியானது 5 இடங்கள் வலப்பக்கமாக நகர்த்தப்பட்டுள்ளது. எனவே, இதன் அறிவியல் குறியீடு 3.794 \times 10^{-5} ஆகும்.
எடுத்துக்கத்தை நினைவில்கொள்க.
| தசமப் புள்ளி வடிவம் | அறிவியல் குறியீடு |
| 1,000 | 1 \times 10^3 |
| 10,000 | 1 \times 10^4 |
| 10,00,000 | 1 \times 10^6 |
| 1,00,00,000 | 1 \times 10^7 |
| 0.001 | 1 \times 10^{-3} |
| 0.00001 | 1 \times 10^{-5} |
| 0.000001 | 1 \times 10^{-6} |
| 0.0000001 | 1 \times 10^{-7} |
| 0.00000001 | 1 \times 10^{-8} |
Register for free to see more content