PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
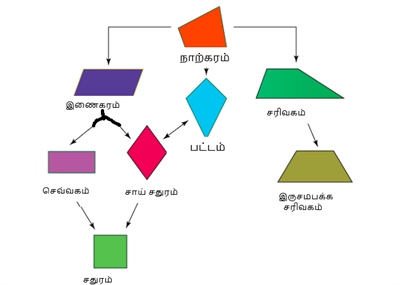
Book Free Demoநாற்கரத்தின் வகைகள்:
- சதுரம்
- செவ்வகம்
- இணைகரம்
- சாய்சதுரம்
- சரிவகம்
- பட்டம்
சதுரம் என்பது நாற்கரமாகும் இவை நான்கு சம பக்கங்கள் மற்றும் நான்கு செங்கோணங்கள் கொண்டவை.
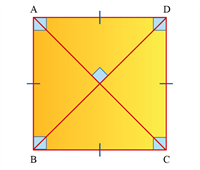
ஒரு சதுரமானது:
-
நான்கு சம பக்கங்கள் \(AB=BC=CD=DA\).
-
நான்கு செங்கோணங்கள் \(∠A=∠B=∠C=∠D=90°\).
-
இரு ஜோடி இணை பக்கங்கள் \(AB∥DC\) மற்றும் \(AD∥BC\).
-
இரு சம மூலைவிட்டங்கள் \(AC=BD\).
-
மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்தானவை \(AC⊥BD\).
-
மூலைவிட்டங்கள் ஒன்றைஒன்று இருசம கூறிடும்.
செவ்வகம் என்பது நாற்கரமாகும் இவை இரு ஜோடி சம மற்றும் இணை பக்கங்கள் மற்றும் நான்கு செங்கோணங்கள் கொண்டவை.
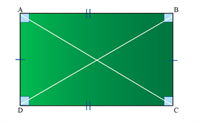
ஒரு செவ்வகமானது:
-
இரு சோடி இணைப் பக்கங்கள் \(AB∥DC\) மற்றும் \(AD∥BC\).
-
நான்கு செங்கோணங்கள் \(∠A=∠B=∠C=∠D=90°\).
-
இரு எதிர் இணைப் பக்கங்கள் \(AB=DC\) மற்றும் \(AD=BC\)
-
இரு சமமூலைவிட்டங்கள் \(AC=BD\)
-
மூலைவிட்டங்கள் ஒன்றைஒன்று இரு சம கூறிடும் .
இணைகரம் என்பது நாற்கரமாகும்.இதன் இரண்டு ஜோடி எதிர் பக்கங்களும் ஒன்றுக்கொன்று இணையாகவும், சமநீளம் கொண்டவை மற்றும் எதிர் கோணங்கள் ஒன்றுக்கொன்று சமமாகும்.
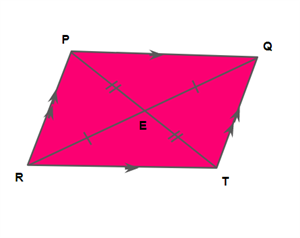
ஒரு இணைகரமானது:
- இரண்டு சோடி இணையான எதிர் பக்கங்களும் \(PQ∥RT\) மற்றும் \(PR∥QT\).
- எதிரெதிர் பக்கங்கள் இணை \(PQ=RT\) மற்றும் \(PR=QT\).
- எதிரெதிர் கோணங்கள் இணை \(∠P=∠T\) மற்றும் \(∠Q=∠R\).
- இரு மூலைவிட்டங்கள் ஒன்றைஒன்று இருசம கூறிடும் .
சரிவகம் என்பது நாற்கரமாகும் இவை ஒரு ஜோடி எதிர்ப்பக்கங்கள் ஒன்றுக்கொன்று இணையாக கொண்டவை.
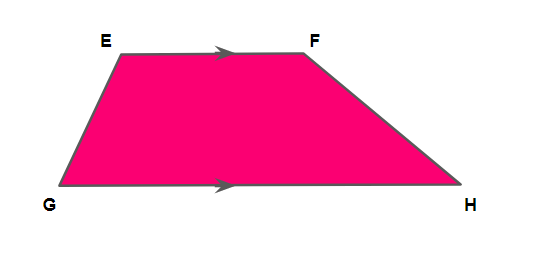
- இரு பக்கங்கள் இணை எனில், அவை தளங்கள் எனப்படும்.
மேற்கண்ட படத்தில் இருந்து, \(EF\) மற்றும் \(GH\) என்பது தளங்கள் ஆகும்.
- இரு இணையற்ற எதிர்ப்பக்கங்கள் கால்கள் எனப்படும்.
மேற்கண்ட படத்தில் இருந்து, \(EG\) மற்றும் \(FH\) என்பது கால்கள் ஆகும்.
இணைகரத்தில் உள்ள பக்கங்கள், கோணங்கள் அல்லது மூலைவிட்டகள் பற்றி வேறெந்த கருத்துக்களும் இல்லை.
ஆனால் இரு இணையற்ற எதிர்ப்பக்கங்கள் சமம் எனில், அவை இருசமபக்க சரிவகம் எனப்படும்.
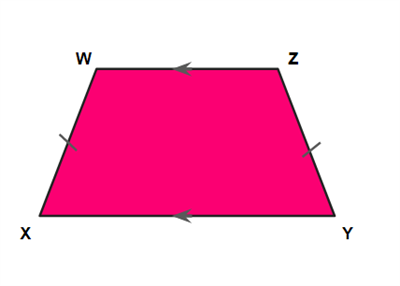
மேற்கண்ட சரிவகம் \(XYZW\) ஒரு இருசமபக்க சரிவகம்.
இருசமபக்க சரிவகத்தின் மூலைவிட்டங்களின் நீளங்கள் சமம். \(XZ=WY\).
சாய்சதுரம் என்பது நற்கரமாகும் இவற்றின் அனைத்து பக்கங்களும் சமம்.
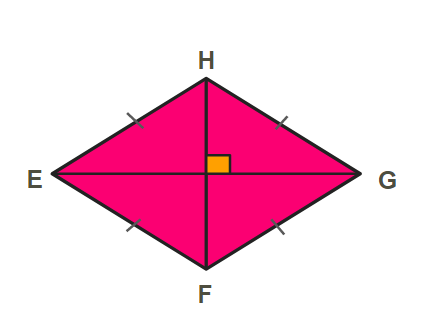
ஒரு சாய்சதுரமானது:
- இரு ஜோடி இணைப்பக்கங்கள் \(EH∥FG\) மற்றும் \(EF∥HG\).
- நான்கு சம பக்கங்கள் \(EH=HG=GF=FE\).
- எதிரெதிர் பக்கங்கள் இணை\(∠E=∠G\) மற்றும் \(∠H=∠F\).
- மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்தானவை \(EG⊥HF\).
- மூலைவிட்டங்கள் ஒன்றுக்கொன்று இருசம கூறிடும்.
பட்டம் என்பது நாற்கரமாகும் இவை இரு ஜோடி சமநீளம் உடைய பக்கங்கள் கொண்டவை.
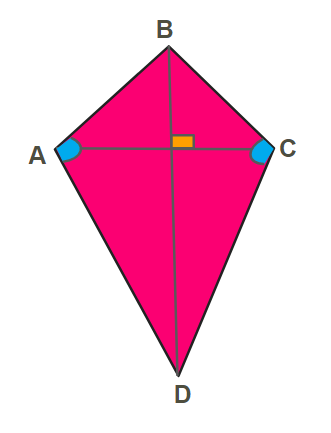
ஒரு பட்டமானது:
- இரு ஜோடி சமநீளம் உடைய பக்கங்கள் \(AB=BC\) மற்றும் \(CD=DA\).
- ஒரு ஜோடி எதிர் கோணங்கள்(விரி கோணம்) சமம் \(∠A=∠C\)
- மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்தானவை \(AC⊥BD\)
- நீளமான மூளைவிட்டம் குட்டையான மூலைவிட்டத்தை வெட்டுகிறது.
இணைக்கரத்தின் வகைகள் பற்றி அறிய கீழ்கண்ட வரைப்படம் உதவுகிறது.
Register for free to see more content