PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoகற்பனையாக:
வட்ட நாற்கரம் ABCD மற்றும் நீட்டிக்கப்பட்ட பக்கம் AB இல் இருந்து E வரை.
இங்கு, கோணங்கள் \angle ABC மற்றும் \angle CBE ஒரே நேர்கோட்டில் அமைந்துள்ள ஜோடிகள்.
நேர்கோட்டில் அமைந்த கோணங்களின் கூடுதல் 180^{\circ}.
அவை, \angle ABC + \angle CBE = 180^{\circ} …… \text{சமன்பாடு}(1)
மேலும், வட்ட நாற்கரத்தின் உள் கோணங்களின் கூடுதல் 180^{\circ}.
அவை, \angle ABC + \angle ADC = 180^{\circ} …… \text{சமன்பாடு}(2)
(1) மற்றும் (2) இல் இருந்து,
\angle ABC + \angle CBE = \angle ABC + \angle ADC
எனவே, \angle CBE = \angle ADC.
இதேபோன்று மற்ற கோணங்களை நிரூபிக்க.
இப்பொழுது முடிவுகள் பின்வருமாறு கொடுக்கப்பட்டுள்ளன.
தேற்றம்: வட்ட நாற்கரத்தின் ஒரு பக்கத்தினை நீட்டிப்பதால் ஏற்படும் வெளிக்கோணம் உள் எதிர்க் கோணத்திற்குச் சமம்.
விளக்கம்:
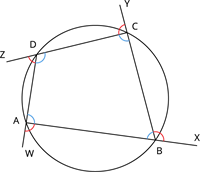
தேற்றத்தின் படி , வட்ட நாற்கரத்தின் ஒரு பக்கத்தினை நீட்டிப்பதால் ஏற்படும் வெளிக்கோணம் உள் எதிர்க் கோணத்திற்குச் சமம்.
இங்கு, படத்தில் இருந்து பக்கம் AB யை Xவரையும், பக்கம் BC யை Yவரையும், பக்கம் CD யை Z வரையும் மற்றும் பக்கம் DAயை W வரையும் நீட்டிக்க . எனவே:
\angle CBX = \angle CDA
\angle DCY = \angle DAB
\angle ADZ = \angle ABC
\angle BAW = \angle BCD
Example:
படத்தில் இருந்து கோணம் z யை காண்க.
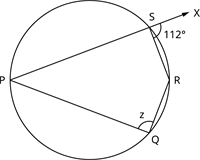
விடை:
தேற்றத்தின் படி, \text{வெளிக்கோணங்கள்} = \text{உள் எதிர்க் கோணங்கள்}.
ஆகவே, \angle RSX = \angle PQR
எனவே, z = 112^{\circ}.
Register for free to see more content