PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoகற்பனையாக:
நாற்கரத்தின் நான்கு முனைகளும் வட்டத்தின் பரிதியைத் தொட்டுக் கொண்டு இருக்குமேயானால்
அந்த நாற்கரம் வட்ட நாற்கரமாகும்.
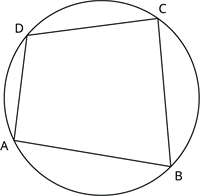
நாற்கரம் ABCD ஒவ்வொரு முனையும் வட்ட மையம் O வின் மேற்பரப்பில் உள்ளது.
ஒவ்வொரு முனையும் O வுடன் இணைப்பதால் சமபக்க முக்கோணங்கள் உண்டாகிறது அவை AOB, BOC, COD மற்றும் DOA இங்கு ஆரங்கள் OA, OB, OC மற்றும் OD.
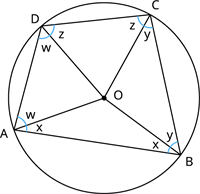
கோணங்கள் வட்ட மையத்தில் ஏற்படுத்தும் கோணம் 360^{\circ}.
மேலும், உள் முக்கோணங்களின் கூடுதல் 180^{\circ}.
எனவே:
அனைத்து சமன்பாடுகளையும் கூட்டுக:
2 (\angle w + \angle x + \angle y + \angle z) + \angle O = 4\மடங்கு 180^{\circ}
2 (\angle w + \angle x + \angle y + \angle z) + 360^{\circ} = 720^{\circ}
2 (\angle w + \angle x + \angle y + \angle z) = 720^{\circ} - 360^{\circ}
2 (\angle w + \angle x + \angle y + \angle z) = 360^{\circ}
\angle w + \angle x + \angle y + \angle z = 180^{\circ}
அதுவே, \angle A + \angle C = 180^{\circ}.
இதேபோன்று, \angle B + \angle D = 180^{\circ}.
இப்பொழுது முடிவுகள் பின்வருமாறு கொடுக்கப்பட்டுள்ளன:.
தேற்றம்: வட்ட நாற்கரத்தின் எதிர்கோணங்கள் மிகைநிரப்புக் கோணங்கள் ஆகும்.
விளக்கம்:
தேற்றத்தின் படி, வட்ட நாற்கரத்தின் எதிர்கோணங்கள் மிகைநிரப்புக் கோணங்கள் ஆகும் 180^{\circ}.
அதுவே, \angle A + \angle C = 180^{\circ}.
மற்றும் \angle B + \angle D = 180^{\circ}.
Example:
படத்தில் இருந்து கோணம் x யை காண்க.
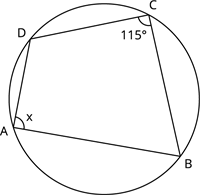
விடை:
தேற்றத்தின் படி, வட்ட நாற்கரத்தின் எதிர்கோணங்கள் மிகைநிரப்புக் கோணங்கள் ஆகும்.
அதுவே:
\angle A + \angle C = 180^{\circ}
x + 115^{\circ} = 180^{\circ}
x = 180^{\circ} - 115^{\circ}
x = 65^{\circ}
தேற்றத்தின் மறுதலை : ஒரு நாற்கரத்தின் ஒரு சோடி எதிர்க்கோணங்கள்
மிகைநிரப்புக் கோணங்கள் எனில் அந்த நாற்கரம் வட்ட நாற்கரமாகும்.
விளக்கம்:
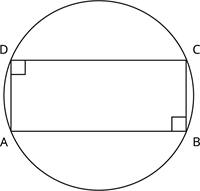
தேற்றத்தின் படி, வட்ட நாற்கரத்தின் உள் கோணங்களின் கூடுதல் 180^{\circ}. இங்கு, படத்தில் இருந்து \angle A மற்றும் \angle C ஆனது 180^{\circ}.
90^{\circ} + 90^{\circ} = 180^{\circ}
நாற்கரம் ABCD ஒரு வட்டநாற்கரம்.
Example:
வட்டத்தின் உள் அமையும் சதுரம் சுழற்சி முறையில் இருக்கும் என நிரூபிக்க.
விளக்கம்:
ஒரு சதுரம் ABCD வட்டத்தில் அமைந்துள்ளது.
சதுரத்தின் ஒவ்வொரு கோணமும் 90^{\circ}.
இங்கு \angle A + \angle C = 90^{\circ} + 90^{\circ}
அதுவே, \angle A + \angle C = 180^{\circ}
இதேபோன்று, \angle B + \angle D = 90^{\circ} + 90^{\circ}
அதுவே, \angle B + \angle D = 180^{\circ}
தேற்றத்தின் படி, ஒரு நாற்கரத்தின் ஒரு சோடி எதிர்க்கோணங்கள்
மிகைநிரப்புக் கோணங்கள் எனில் அந்த நாற்கரம் வட்ட நாற்கரமாகும்.
வட்டத்தின் உள் அமையும் சதுரம் சுழற்சி முறையில் இருக்கும் என நிரூபிக்கப்பட்டது.
Register for free to see more content