PDF chapter test TRY NOW
ஒரு செங்கோண முக்கோணத்திலுள்ள இரு குறுங்கோணங்களின் கூடுதல் 90^{\circ} எனில், இரு குறுங்கோணங்கள் எப்பொழுதுமே ஒன்றுக்கொன்று
நிரப்புக் கோணங்கள் ஆகும்.
நிரப்புக் கோணங்கள் ஆகும்.
செங்கோண முக்கோணத்திலுள்ள இரு குறுங்கோணங்களின் கூடுதல் 90^{\circ}.
இரு குறுங்கோணங்கள் எப்பொழுதுமே ஒன்றுக்கொன்று நிரப்புக் கோணங்கள் ஆகும்.
முக்கோணம் PQR ஆனது P இல் செங்கோணம்.
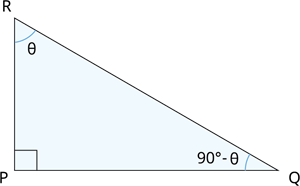
இங்கு R மற்றும் Q என்பன நிரப்பு கோணங்கள்.
எனவே, \angle R = \theta எனில், \angle Q = 90^{\circ} - \theta.
முக்கோணவியலின் விகிதங்கள் \angle R = \theta கான அட்டவணை.
அட்டவணை 1:
முக்கோணவியலின் விகிதங்கள் | தொடர்பு \Delta PQR | முக்கோணவியலின் விகிதம் | தொடர்பு \Delta PQR |
\sin \theta | \sin \theta = \frac{PQ}{RQ} | \text{cosec}\,\theta | \text{cosec}\,\theta = \frac{RQ}{PQ} |
\cos \theta | \cos \theta = \frac{PR}{RQ} | \sec \theta | \sec \theta = \frac{RQ}{PR} |
\tan \theta | \tan \theta = \frac{PQ}{PR} | \cot \theta | \cot \theta = \frac{PR}{PQ} |
முக்கோணவியலின் விகிதங்கள் \angle Q = 90^{\circ} - \theta .
அட்டவணை 2:
முக்கோணவியலின் விகிதங்கள் | தொடர்பு \Delta PQR | முக்கோணவியலின் விகிதங்கள் | தொடர்பு \Delta PQR |
\sin (90^{\circ} - \theta) | \sin (90^{\circ} - \theta) = \frac{PR}{RQ} | \text{cosec}\,(90^{\circ} - \theta) | \text{cosec}\,(90^{\circ} - \theta) = \frac{RQ}{PR} |
\cos (90^{\circ} - \theta) | \cos (90^{\circ} - \theta) = \frac{PQ}{RQ} | \sec (90^{\circ} - \theta) | \sec (90^{\circ} - \theta) = \frac{RQ}{PQ} |
\tan (90^{\circ} - \theta) | \tan (90^{\circ} - \theta) = \frac{PR}{PQ} | \cot (90^{\circ} - \theta) | \cot (90^{\circ} - \theta) = \frac{PQ}{PR} |
அட்டவணை 1 மற்றும் 2 இல் இருந்து, கீழ்கண்டவற்றை பெறலாம்.
1. \sin \theta = \cos (90^{\circ} - \theta)
2. \cos \theta = \sin (90^{\circ} - \theta)
3. \tan \theta = \cot (90^{\circ} - \theta)
4. \text{cosec}\,\theta = \sec (90^{\circ} - \theta)
5. \sec \theta = \text{cosec}(90^{\circ} - \theta)
6. \cot \theta = \tan (90^{\circ} - \theta)
Register for free to see more content