PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoமுக்கோணவியல் விகிதங்கள் - கோண அளவு 90^{\circ} ஒரலகு வட்டத்தினை பயன்படுத்தி காண்க.
ஓரலகு வட்டம் என்பது ஆதிப்புள்ளியை மையமாகவும், ஆரம் 1 அலகும் கொண்ட ஒரு வட்டம் ஆகும்.
இங்கு OQ = OP = OC = 1 அலகு (ஆரம்).
முதற் காற்பகுதியில்
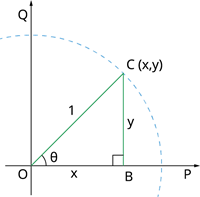
C(x,y) என்பது வட்டத்தின் மீது அமைந்த புள்ளி மற்றும் \angle COB = \theta.
செங்கோண முக்கோணம் COB இல் இருந்து:
எதிர் பக்கம் = y
அடுத்துள்ள பக்கம் = x
கர்ணம் = 1
முதற் காற்பகுதியில் அமைந்த புள்ளிகளை C கொண்டு முக்கோணவியலின் விகிதங்களை காண்க.
- Sine \theta:
\sin \theta = \frac{\text{எதிர் பக்கம்}}{\text{கர்ணம்}}
= \frac{y}{1}
= y
- Cosine \theta:
\cos \theta = \frac{\text{அடுத்துள்ள பக்கம்}}{\text{கர்ணம்}}
= \frac{x}{1}
= x
- Tangent \theta:
\tan \theta = \frac{\text{எதிர் பக்கம்}}{\text{அடுத்துள்ள பக்கம்}}
= \frac{y}{x}
கோண அளவு \theta = 90^{\circ}, OC ஆனது OQ இல் சந்திக்கிறது, எனில் Q = (0,1) இங்கு x = 0 மற்றும் y = 1.
முக்கோணவியலின் விகிதங்கள்:
- Sine 90^{\circ}:
\sin 0^{\circ} = y
= 1
- Cosine 90^{\circ}:
\cos 90^{\circ} = x
= 0
- Tangent 90^{\circ}:
\tan 90^{\circ} = \frac{1}{0}
= வரையறுக்க படவில்லை
முக்கோணவியலின் தலைகீழிகள்:
- Cosecant 90^{\circ}:
\text{cosec}\,90^{\circ} = \frac{1}{\sin 90^{\circ}}
= \frac{1}{1}
= 1
- Secant 90^{\circ}:
\sec 90^{\circ} = \frac{1}{\cos 90^{\circ}}
= \frac{1}{0}
= வரையறுக்க படவில்லை
- Cotangent 90^{\circ}:
\cot 90^{\circ} = \frac{1}{\tan 90^{\circ}}
= \frac{0}{1}
= 0
முக்கோணவியல் விகிதங்கள் - கோண அளவு 90^{\circ} கான அட்டவணை.
\sin \theta | \cos \theta | \tan \theta | \text{cosec}\,\theta | \sec \theta | \cot \theta | |
\theta = 90^{\circ} | 1 | 0 | வரையறுக்க படவில்லை | 1 | வரையறுக்க படவில்லை | 0 |
Register for free to see more content