PDF chapter test TRY NOW
Result \(4\):
If two circles touch externally, the distance between their centres equals the sum of their radii.
Explanation:
 |
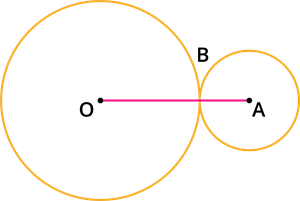If two circles touch externally at a point \(B\), then the distance \(OA\) is equal to the sum of the radii \(OB\) and \(AB\).
\(\Rightarrow\) \(OA\) \(=\) \(OB\) \(+\) \(AB\)
Proof of the result:
Let the two circles with centres \(O\) and \(A\) intersect each other externally at point \(B\).
Let the radius \(OB\) \(=\) \(r_{1}\) and \(AB\) \(=\) \(r_{2}\) and \(r_{1}\) \(>\) \(r_{2}\).
Let the distance between the centres be \(d\).
\(\Rightarrow\) \(OA\) \(=\) \(d\)
From the figure, we observe that \(OA\) \(=\) \(OB\) \(+\) \(AB\).
\(\Rightarrow\) \(d\) \(=\) \(r_{1}\) \(+\) \(r_{2}\)
Example:
Two circle with radii \(4\) \(cm\) and \(5\) \(cm\) intersect at a point \(O\) externally. If so, find the distance between their centres.
Solution:
By the result, we know that:
Distance between the centres \(=\) Sum of the radii.
Thus, the distance between the centres \(=\) \(4\) \(cm\) \(+\) \(5\) \(cm\)
\(=\) \(9\) \(cm\)
Register for free to see more content