UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreStatement:
(i) If \(A\) and \(B\) are any two non mutually exclusive events then:
\(P(A \cup B)\) \(=\) \(P(A)\) \(+\) \(P(B)\) \(-\) \(P(A \cap B)\)
(ii) If \(A\), \(B\)and \(C\) are any three non mutually exclusive events then:
\(P(A \cup B \cup C)\) \(=\) \(P(A)\) \(+\) \(P(B)\) \(+\) \(P(C)\) \(-\) \(P(A \cap B)\) \(-\) \(P(B \cap C)\) \(-\) \(P(A \cap C)\) \(+\) \(P(A \cap B \cap C)\)
Proof of the theorem:
Statement (i):
Let \(A\) and \(B\) be any two events of a random experiment.
Let \(S\) be its sample space.
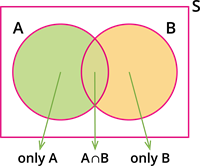
From the Venn diagram, we observe that the events only \(A\), only \(B\) and \(A \cap B\) are mutually exclusive.
The union of these three events is \(A \cup B\).
Therefore, \(P(A \cup B)\) \(=\) \(P(\text{only }A) + P(A \cap B) + P(\text{only }B)\).
(i) \(P(A \cap \overline B)\) \(=\) \(P(\text{only A})\) \(=\) \(P(A) - P(A \cap B)\)
(ii) \(P(\overline A \cap B)\) \(=\) \(P(\text{only B})\) \(=\) \(P(B) - P(A \cap B)\)
\(\Rightarrow\) \(P(A \cup B)\) \(=\) \(\left[P(A) - P(A \cap B)\right] + P(A \cap B) + \left[P(B) - P(A \cap B)\right]\)
\(\Rightarrow\) \(P(A \cup B)\) \(=\) \(P(A) + P(B) - P(A \cap B)\)
Hence, the proof.
Statement (ii):
Let \(A\), \(B\) and \(C\) be any three events of a random experiment.
Let \(S\) be its sample space.
Let \(D\) \(=\) \(B \cup C\).
Thus, \(P(A \cup B \cup C)\) \(=\) \(P(A \cup D)\).
\(\Rightarrow\) \(P(A \cup B \cup C)\) \(=\) \(P(A) + P(D) - P(A \cap D)\) [By statement (i)]
\(=\) \(P(A) + P(B \cup C) - P\left[A \cap (B \cup C)\right]\)
\(=\) \(P(A) + \left[P(B) + P(C) - P(B \cap C)\right] - P\left[(A \cap B) \cup (A \cap C)\right]\)
\(=\) \(P(A) + P(B) + P(C) - P(B \cap C) - \left[P(A \cap B) + P(A \cap C) - P\left((A \cap B) \cap (A \cap C)\right)\right]\)
\(=\) \(P(A) + P(B) + P(C) - P(B \cap C) - P(A \cap B) - P(A \cap C) + P(A \cap B \cap C)\)
Therefore,
\(P(A \cup B \cup C)\) \(=\) \(P(A)\) \(+\) \(P(B)\) \(+\) \(P(C)\) \(-\) \(P(A \cap B)\) \(-\) \(P(B \cap C)\) \(-\) \(P(A \cap C)\) \(+\) \(P(A \cap B \cap C)\).
Hence, the proof.
Register for free to see more content