PDF chapter test TRY NOW
We will derive the trigonometric ratios of 0^{\circ} with the help of a unit circle.
A circle with radius 1 unit centred at the origin is called a unit circle.
Here OQ = OP = OC = 1 unit (Radius).
Let us consider the first quadrant.
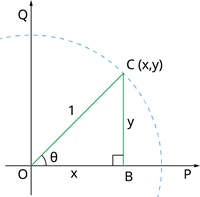
Let the point C(x,y) be any point on the unit circle and \angle COB = \theta.
In the right angles triangle COB we have:
Opposite side = y
Adjacent side = x
Hypotenuse = 1
Now, let us determine the trigonometric ratios in the first quadrant with the coordinate C.
- Sine \theta:
\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}
= \frac{y}{1}
= y
- Cosine \theta:
\cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}}
= \frac{x}{1}
= x
- Tangent \theta:
\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}
= \frac{y}{x}
When \theta = 0^{\circ}, OC coincides with OP then P = (1,0) where x = 1 and y = 0.
Then the trigonometric ratios are given by:
- Sine 0^{\circ}:
\sin 0^{\circ} = y
= 0
- Cosine 0^{\circ}:
\cos 0^{\circ} = x
= 1
- Tangent 0^{\circ}:
\tan 0^{\circ} = \frac{0}{1}
= 0
Using these basic trigonometric ratios determine their reciprocals as follows:
- Cosecant 0^{\circ}:
\text{cosec}\,0^{\circ} = \frac{1}{\sin 0^{\circ}}
= \frac{1}{0}
= not defined
- Secant 0^{\circ}:
\sec 0^{\circ} = \frac{1}{\cos 0^{\circ}}
= \frac{1}{1}
= 1
- Cotangent 0^{\circ}:
\cot 0^{\circ} = \frac{1}{\tan 0^{\circ}}
= \frac{1}{0}
= not defined
Let us summarize all the trigonometric ratios of 0^{\circ} in the following table.
\sin \theta | \cos \theta | \tan \theta | \text{cosec}\,\theta | \sec \theta | \cot \theta | |
\theta = 0^{\circ} | 0 | 1 | 0 | not defined | 1 | not defined |
Register for free to see more content